- 真题试卷
- 模拟试卷
- 预测试卷
1.集合
A
B
C
D
正确答案
解析
因为
所以
知识点
2.
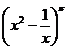
正确答案
解析
由已知得：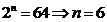
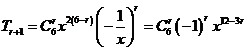
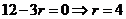
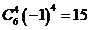
知识点
8.在平行四边形ABCD中，
正确答案
解析
由题意可知
因为
所以（2R）2=AC2=AB2+BD2+CD2=2AB2+BD2=4，R2=1，S=4πr2=4π；
故选C
知识点
10.已知抛物线
A
B
C3
D2
正确答案
解析
设
知识点
3.已知
A
B
C
D
正确答案
解析
略
知识点
4.将函数
A
B
C
D
正确答案
解析
将函数
知识点
9.下面命题中假命题是（ ）
A∀x∈R，3x＞0
B∃α，β∈R，使sin（α+β）=sinα+sinβ
C∃m∈R，使
D命题“∃x∈R，x2+1＞3x”的否定是“∀x∈R，x2+1＞3x”
正确答案
解析
A，根据指数函数的性质可知，∀x∈R，3x＞0，∴A正确．
B，当α=β=0时，满足sin（α+β）=sinα+sinβ=0，∴B正确．
C，当m=1时，幂函数为f（x）=x3，且在（0，+∞）上单调递增，∴C正确．
D，命题“∃x∈R，x2+1＞3x”的否定是“∀x∈R，x2+1≤3x”，∴D错误．
故选：D.
知识点
5.执行如图所示的程序框图，会输出一列数，则这个数列的第3项是（ ）
正确答案
解析
当N=1时，A=3，故数列的第1项为3，N=2，满足继续循环的条件，A=3×2=6；当N=2时，A=6，故数列的第2项为6，N=3，满足继续循环的条件，A=6×5=30；当N=3时，A=30，故数列的第3项为30，故选：B.
知识点
7.在等腰
A
B
C
D
正确答案
解析
知识点
6.有5名优秀毕业生到母校的3个班去作学习经验交流，则每个班至少去一名的不同分派方法种数为（ ）
A
B
C
D
正确答案
解析
人数分配上有两种方式即1，2，2与1，1，3．
若是1，1，3，则有
所以共有150种不同的方法．故选：A.
知识点
11.若复数
正确答案
解析
∵复数
∴
故答案为：
知识点
14.已知直线
正确答案
解析
由题意得，圆的半径为3，且圆心到直线的距离为
根据圆的弦长公式可知
知识点
13.如图，某海事部门举行安保海上安全演习．为了测量正在海面匀速行驶的某航船的速度，在海岸上选取距离为1千米的两个观察点C，D，在某天10：00观察到该航船在A处，此时测得∠ADC＝30°，3分钟后该船行驶至B处，此时测得∠ACB＝60°，∠BCD＝45°，∠ADB＝60°，则船速为___________千米/分钟. （用含根号的式子表示）
正确答案
解析
略
知识点
15.定义全集
①若
②对于任意
③对于任意
④对于任意
其中正确的结论有 ．（写出全部正确结论的序号）
正确答案
①②③
解析
∵
而CUA中可能有B的元素，但CUB中不可能有A的元素
∴
对于B，∵
结合fA（x）的表达式，可得f∁UA（x）=1﹣fA（x），故②正确；
对于C，fA∩B（x）=
故③正确；
对于D，fA∪B（x）=
当某个元素x在A中但不在B中，由于它在A∪B中，故fA∪B（x）=1，
而fA（x）=1且fB（x）=0，可得fA∪B（x）≠fA（x）•fB（x）
由此可得④不正确．
故答案为：①②③．
知识点
12.如果函数f（x）=
正确答案
﹣1
解析
∵函数f（x）是奇函数，
∴f（﹣2）=﹣f（2）=﹣（2×2﹣3）=﹣1，
故答案为：﹣1
知识点
16.已知函数
（1）求函数
（2）设
正确答案
（1）
（2）
解析
（1）由图象可知
（2）∵
又∵
∵
∴
知识点
17.随机变量X的分布列如下表如示，若数列
（1）求随机变量X的分布列；
（2）一个盒子里装有标号为1，2，…，n且质地相同的标签若干张，从中任取1张标签所得的标号为随机变量X．现有放回的从中每次抽取一张，共抽取三次，求恰好2次取得标签的标号不大于3的概率．
正确答案
见解析。
解析
（1）依题意得，数列
（2）随机抽取一次取得标签的标号不大于3的概率为
所以恰好2次取得标签的标号小于3的概率为
知识点
21.已知函数
（1）若
（2）若对于任意的
正确答案
（1）2<a<4
（2）
解析
（1）解：
（2）解法1：
（i）当
所以
（ii）当
综上，
故
解法2：
等号当且仅当
又
解法3：
且上述两个不等式的等号均为
知识点
19.已知数列
（1）设
（2）（i）求数列
（ii）求证：对于任意
正确答案
见解析。
解析
（1）由已知得
则
又
（2）（i）解法1：由（I）得
相减得
则
相加得
当
由
故
解法2：由
则
相加得
解法3：由
设
又
则
（ii）证法1：易证
则
同理可得
则
故
证法2：
故
证法3：
易证
则
故
知识点
20.已知椭圆C：
（1）求椭圆C的离心率；
（2）设b=2，直线y=kx+4与椭圆C交于不同的两点M，N，求证：直线BM与直线AN的交点G在定直线上．
正确答案
（1）
（2）见解析
解析
（1）设F的坐标为(–c，0)，依题意有bc=
∴椭圆C的离心率e=
（2）若b=2，由（Ⅰ）得a=2
联立方程组
化简得：(2k2+1)x2+16kx+24=0，
由△=32(2k2–3)＞0，解得：k2＞
由韦达定理得：xM+xN=
设M(xM，kxM+4)，N(xN，kxN+4)，
MB方程为：y=
NA方程为：y=
由③④解得：y=
=
即yG=1，
∴直线BM与直线AN的交点G在定直线上
知识点
18.如图，四棱锥
（1）求证：
（2）求点
（3）求直线
正确答案
见解析。
解析
如图建立空间直角坐标系如图，则A（0，0，0），P（0，0，3），D（0，3，0），E（
（1）取PC的中点G，连结EG，则G
（2）设平面PCE的法向量为
（3）
