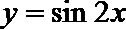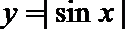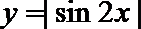理科数学浦东新区2013年高三试卷

精品

填空题
单选题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、填空题

2、单选题

3、简答题

真题试卷
模拟试卷
预测试卷

填空题本大题共14小题，每小题4分，共56分。把答案填写在题中横线上。

题型：填空题

分值: 4分

1．已知全集，，，则（）。

正确答案

（0，1）

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

题型：填空题

分值: 4分

2．若，则（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 4分

5．在二项式的展开式中，含的项的系数为（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：填空题

分值: 4分

6．函数的最小正周期是（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

题型：填空题

分值: 4分

7．设函数，则实数的取值范围是（）。

正确答案

（-3，1）

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 4分

11．对于任意，不等式恒成立，则实数的取值范围是（）。

正确答案

（-∞，-1）（3，+∞）

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

题型：填空题

分值: 4分

12．设函数在内有定义，对于给定的正数K，定义函数

，若函数。当=时，函数的单调递增区间为（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 4分

3．若的反函数，则（）。

正确答案

-1

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 4分

10．已知函数定义域为是偶函数，则函数的值域为（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 4分

4．函数的单调递减区间是（）。

正确答案

（2，+∞）

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：填空题

分值: 4分

13．已知函数

①；

②；

③；

④

其中对于定义域内的任意一个自变量，都存在定义域内的唯一一个自变量，使得成立的函数是（）。

正确答案

③

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 4分

9．从0，2，4中取一个数字，从1，3，5中取两个数字，组成无重复数字的三位数，从这些三位数中任取一个，则所取的三位数为偶数的概率是（）（用分数作答）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：填空题

分值: 4分

14．已知定义在R上的奇函数，满足,且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间上有四个不同的根,则（）。

正确答案

-8

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：填空题

分值: 4分

8．定义在上的函数既是偶函数又是周期函数，若的最小正周期为，且当时，，则的值是（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

相等向量与相反向量

单选题本大题共4小题，每小题4分，共16分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 4分

18．已知函数的图像与函数（且）的图像交于点，如果，那么的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 4分

15．设集合，集合，且，则实数的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

题型：单选题

分值: 4分

16．设函数的反函数为，对于内的所有的值，下列关系式中一定成立的是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 4分

17．在下列函数中，既是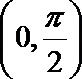上的增函数，又是以为最小正周期的偶函数的函数是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的判断与证明函数奇偶性的判断函数的周期性

简答题（综合题）本大题共78分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

19．在中，是角所对的边，是该三角形的面积，且．

（1）求角；

（2）若，求的值．

正确答案

（1）由已知等式得：

（2）

解析

解析已在路上飞奔，马上就到！

知识点

三角函数中的恒等变换应用

题型：简答题

分值: 16分

21．为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层．某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能源消耗费用C（单位：万元）与隔热层厚度（单位：cm）满足关系：，若不建隔热层，每年能源消耗费用为8万元．设为隔热层建造费用与20年的能源消耗费用之和．

（1）求的值及的表达式；

（2）隔热层修建多厚对，总费用达到最小，并求最小值．

正确答案

（1）k=40

（2）

当且仅当即时，有最小值70万元。

解析

解析已在路上飞奔，马上就到！

知识点

函数的图象与图象变化

题型：简答题

分值: 14分

20．已知函数满足对任意恒成立，在R上单调递减。

（1）求证：是奇函数；

（2）若对一切，关于的不等式恒成立，求实数的取值范围。

正确答案

（1）是奇函数

（2）∵函数是奇函数，且在R上单调递减，

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 18分

23．已知函数满足，是不为的实常数。

（1）若当时，，求函数的值域；

（2）若当时，，求函数的解析式；

（3）若当时，，试研究函数在区间上是否可能是单调函数？若可能，求出的取值范围；若不可能，请说明理由。

正确答案

（1）

（2）当时，

（3）当时，

显然时是增函数，

此时，，

若函数在区间上不是单调函数；

所以

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

题型：简答题

分值: 18分

22．阅读下面题目柯西不等式的解法，再根据要求解决后面的问题.

阅读题目：对于任意实数，证明不等式

. （柯西不等式）

证明：构造函数

注意到，所以，

即.（其中等号成立当且仅当，即.）

问题：

（1）请用柯西不等式的结论证明：对任意正实数，不等式成立.

（2）对任意正实数，由（1）知不等式成立，利用此不等式求函数的最小值，并指出此时的值.

（3）根据阅读题目的证明，将不等式进行推广，得到一个更一般的不等式，并用构造函数的方法对你的推广进行证明。

正确答案

（1）因为都是正实数，由已知不等式得

所以不等式成立。

（其中等号成立当且仅当，即）

（2）因为0<，所以

（其中等号成立当且仅当即）

所以函数有最小值25，此时。

（3）可将不等式推广到元的情形，即对于任意实数

，

不等式

成立

证明如下：

设

注意到恒成立，所以

即

其中等号成立当且仅当，

即

解析

解析已在路上飞奔，马上就到！

知识点

平行公理

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷