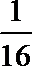- 真题试卷
- 模拟试卷
- 预测试卷
3．m、n为两条不重合的直线，α、β为两个不重合的平面，则下列命题中正确的是（ ）
①若m、n都平行于平面α，则m、n一定不是相交直线；
②若m、n都垂直于平面α，则m、n一定是平行直线；
③已知α、β互相垂直，m、n互相垂直，若m⊥α，则n⊥β；
④m、n在平面α内的射影互相垂直，则m、n互相垂直
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．已知抛物线C：y＝
A
B
C
D
正确答案
解析
知识点
2．设z＝1－i （i是虚数单位），则
正确答案
解析
知识点
9．在二项式
A
B
C
D
正确答案
解析
知识点
1．已知全集U＝R，集台M＝{x｜
AM∩N＝M
BM∪N＝N
CM∩（CUN）＝
D（CUM）∩N＝
正确答案
解析
知识点
5．已知某随机变量X的概率密度函数为P（x）＝
A
B
C
D
正确答案
解析
知识点
8．已知sinα－sinβ＝
A
B
C
D
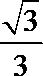
正确答案
解析
知识点
7．已知数列{
A
B
C
D
正确答案
解析
知识点
10．从1开始的自然数按如图所示的规则排列，现有一个三角形框架在图中上下或左右移动，使每次恰有九个数在此三角形内，则这九个数的和可以为（ ）
正确答案
解析
知识点
12．已知定义在（0，＋∞）上的单调函数f（x），对
A（1，2）
B（2，3）
C（
D（0，
正确答案
解析
知识点
11．已知椭圆
A3
B2
C1
D
正确答案
解析
知识点
6．在平面直角坐标平面上,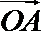 
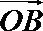
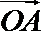
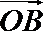
A－
B
C
D
正确答案
解析
知识点
14．若点（1，1）在不等式组
正确答案
解析
知识点
15．已知某个几何体的三视图如下，根据图中标出的尺寸，可得这个几何体的外接球的表面积是___________．
正确答案
164π
解析
知识点
13．设正项等比数列{
正确答案
15
解析
知识点
16．已知定义在R上的函数f（x）是奇函数且满足f（
正确答案
-5
解析
知识点
19．第22届索契冬奥会期间，来自俄罗斯国际奥林匹克大学的男、女大学生共9名志愿者被随机地平均分配到速滑、冰壶、自由式滑雪这三个岗位服务，且速滑岗位至少有一名女大学生志愿者的概率是
（Ⅰ）求冰壶岗位至少有男、女大学生志愿者各一人的概率；
（Ⅱ）设随机变量X为在自由式滑雪岗位服务的男大学生志愿者的人数，求X的分布列及期望．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18． AB为圆O的直径，点E、F在圆上，AB∥EF，矩形ABCD所在平面与圆O所在平面互相垂直，已知AB＝2，BC＝EF＝1．
（Ⅰ）求证：BF⊥平面DAF；
（Ⅱ）求平面ADF与平面CDFE所成的二面角的余弦值．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
21． 已知函数f（x）＝（nx－n＋2）·
（Ⅰ）求f（x）在[0，1]上的最大值；
（Ⅱ）若函数g（x）＝
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
请在第22~24题中任选一题做答。
22.选修4—1：几何证明选讲
如图，△ABC内接于⊙O，AB＝AC，直线MN切⊙O于点C，弦BD∥MN，AC与BD相交于点E．
（Ⅰ）求证：△ABE≌△ACD；
（Ⅱ）若AB＝6，BC＝4，求AE．
23．选修4—4：坐标系与参数方程
已知曲线C的极坐标方程为ρ＝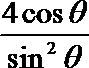
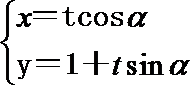
（Ⅰ）把曲线C的极坐标方程和直线l的参数方程化为直角坐标方程，并说明曲线C的形状；
（Ⅱ）若直线l经过点（1，0），求直线l被曲线C截得的线段AB的长．
24．选修4—5：不等式选讲
设函数f（x）＝｜2x－1｜＋｜ax－3｜，x∈R．
（Ⅰ）若a＝1时，解不等式f（x）≤5；
（Ⅱ）若a＝2时，g（x）＝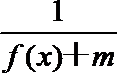
正确答案
22.
23.
24.
解析
解析已在路上飞奔，马上就到！
知识点
17．如图所示，扇形AOB，圆心角AOB的大小等于
（Ⅰ）若
（Ⅱ）设∠COP＝θ，求线段CP与线段OC的长度的和的最大值及此时θ的值．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20． 已知圆N：
（Ⅰ）当直线l的斜率为－1时，求线段AB的长；
（Ⅱ）设点M点N关于直线y＝x对称，问是否存在直线l，使得
正确答案
解析
解析已在路上飞奔，马上就到！