- 真题试卷
- 模拟试卷
- 预测试卷
3.下列命题中是假命题的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 已知数列
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.边长为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.定义在R上的函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.正项等比数列


正确答案
16
解析
解析已在路上飞奔,马上就到!
知识点
9.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知
正确答案
10
解析
解析已在路上飞奔,马上就到!
知识点
12. 设函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.定义一种运算



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 已知函数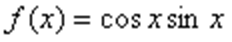
①若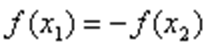
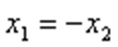
②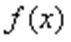
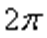
③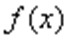
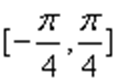
④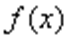
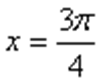
其中正确说法的序号是__________.
正确答案
③④
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数

(1)若

(2)若函数



(3)若

正确答案
(1)解:当


由

由


所以函数



(2)解:因为
由题意得:

即

设

所以当


因为对任意

所以


所以,实数


(3)
解析
解析已在路上飞奔,马上就到!
知识点
20.已知A(






(1)求



(2)已知






(3)在(2)的条件下,设









正确答案
解:
(1)∵点M在直线x=

又



∴

① 当






② 当







综合①②得,

(Ⅱ)由(Ⅰ)知,当


∴

n≥2时,




①+②得,2

当n=1时,


(Ⅲ)













∴

当c=1时,
∴1<
∴m=1.
解析
解析已在路上飞奔,马上就到!
知识点
15. 如图,在平面直角坐标系





(1)求
(2)求
正确答案
(1)由已知得:
∵
∴
∴ 
∴
(2)∵
∴

∴
∴
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(1)求
(2)求
(3)当

正确答案
(1)
令
∴

(2)
故

(3) 






解析
解析已在路上飞奔,马上就到!
知识点
17.设等差数列

(1)若

(2)若

正确答案
(1)由
又
故解得
因此,

(2)由
即
由①+②得-7d<11,即
由①+③得

于是


将4代入①②得
又
所以,所有可能的数列

解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数

(1)求
(2)设不等式




(3)已知






正确答案
(1)
由



(2)

由

令

又

(3)设存在公差为









故
②-①×2得,

故



解析
解析已在路上飞奔,马上就到!










































































