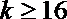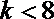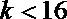- 真题试卷
- 模拟试卷
- 预测试卷
2.已知集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.给出下列命题:
①向量





②


③将函数


④若

以上命题正确的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.有下列四种说法:
①命题:“



②已知随机变量



③函数


④设实数


其中错误的个数是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
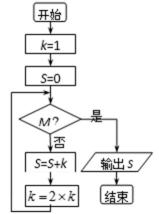
3.按照如图的程序框图
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知某几何体的正视图和侧视图均是边长为1的正方形,则这个几何体的体积不可能是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
选做题(任选两题,若多选,按前两题答案计分)
9.如图,割线PBC经过圆心O,PB=OB=1,OB绕点O逆时针旋转120°到OD,连结PD交圆O于点E,则PE=____________。

10.若直线的极坐标方程为




11.若不等式



正确答案
9. 
10. 
11. 
解析
解析已在路上飞奔,马上就到!
知识点
12.设


正确答案
60
解析
解析已在路上飞奔,马上就到!
知识点
13.设实数x,y满足条件:1




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.设数列








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知点F为抛物线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设集合





(1)
(2)设集合



正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
17.在




(1)求角
(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.在2012年“双节”期间,高速公路车辆较多。某调查公司在一服务区从七座以下小型汽车中,按进服务区的先后每间隔50辆就抽取一辆的抽样方法,抽取了40名驾驶员进行调查,
将他们在某段高速公路上的车速(km/t)分成6段:





问:
(1)该公司在调查取样中,用到的是什么抽样方法?
(2)求这40辆小型汽车车速的众数和中位数的估计值;
(3)若从车速在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,在三棱锥









(1)求证:

(2)求证:
(3)求二面角
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,某隧道设计为双向四车道,车道总宽20m,要求通行车辆限高5m,隧道全长2.5km,隧道的两侧是与地面垂直的墙,高度为3米,隧道上部拱线近似地看成半个椭圆。
(1)若最大拱高h为6 m,则隧道设计的拱宽
(2)若要使隧道上方半椭圆部分的土方工程 量最小,则应如何设计拱高h和拱宽



(3)为了使隧道内部美观,要求在拱线上找两个点M.N,使它们所在位置的高度恰好是限高5m,现以M.N以及椭圆的左.右顶点为支点,用合金钢板把隧道拱线部分连接封闭,形成一个梯形,若l=30m,梯形两腰所在侧面单位面积的钢板造价是梯形顶部单位面积钢板造价的

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆C的中心在原点,离心率等于

(1)求椭圆C的方程;
(2)已知P(2,3).Q(2,-3)是椭圆上的两点,A,B是椭圆上位于直线PQ两侧的动点,
①若直线AB的斜率为
②当A.B运动时,满足

试问直线AB的斜率是否为定值,请说明理由。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数

(1)当

(2)求函数

(3)在(1)的条件下,设




参考数据:
正确答案
解析
解析已在路上飞奔,马上就到!