- 真题试卷
- 模拟试卷
- 预测试卷
1.若复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.与双曲线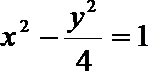
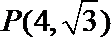
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.程序框图如下,若恰好经过
正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
9. 在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.先后抛掷两枚质地均匀的骰子(各个面上分别标有


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.如图是青年歌手电视大奖赛上某一位选手的得分茎叶图,若去掉一个最高分和一个最低分后,则剩下数据的方差

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知直线


①若

②若

③若

④若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知两圆





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.数列



正确答案
解析
假设
∵
∴






知识点
13.点




正确答案
6
解析
解析已在路上飞奔,马上就到!
知识点
14.某建筑公司要在一块宽大的矩形地面(如图所示)上进行开发建设,阴影部分为一公共设施建设不能开发,且要求用栏栅隔开(栏栅要求在一直线上),公共设施边界为曲线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在三棱柱



(1)求证:平面

(2)如果



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某人准备购置一块占地



(1)试用

(2)若要使

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.设函数
(1)求
(2)讨论函数
(3)设函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在





(1)若


(2)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设椭圆






(1)求椭圆
(2)设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知等比数列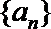
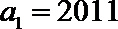

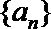
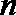
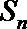
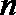
(1)证明: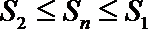
(2)判断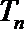
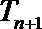
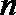
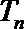
(3)证明:若数列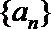
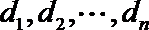
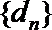
正确答案
解析
解析已在路上飞奔,马上就到!