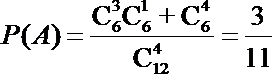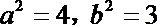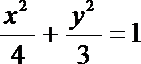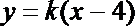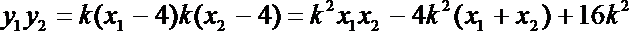- 真题试卷
- 模拟试卷
- 预测试卷
2.投掷两颗骰子,其向上的点数分别为


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.阅读下面的程序框图,则输出的
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知两点



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.在实验室进行的一项物理实验中,要先后实施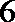
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.某学生四次模拟考试时,其英语作文的减分情况如下表:
显然所减分数y与模拟考试次数x之间有较好的线性相关关系,则其线性回归方程为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.过抛物线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知定义在










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知把向量a﹦(1,1)向右平移两个单位,再向下平移一个单位得到向量b,则b的坐标为____________
正确答案
(1,1)
解析
解析已在路上飞奔,马上就到!
知识点
13.已知点P的坐标


正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
14.设二次函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.若某几何体的三视图 (单位:cm) 如图所示,则此几何体的表面积是____________cm
正确答案
6+(
解析
解析已在路上飞奔,马上就到!
知识点
15.((1)、(2)小题选做一题)
(1)如图,圆O的直径AB=8,C为圆周上一点,BC=4,过点C作圆的切线l,过点A作直线l的垂线AD,D为垂足,AD与圆O交于点E,则线段AE的长为____________.
(2)在平面直角坐标系下,曲线


正确答案
(1)4;
(2)
解析
解析已在路上飞奔,马上就到!
知识点
17.在数列
(1)求数列

(2)若存在


正确答案
解:(1)
(2)
由(1)可知当
设
则
又

所以所求实数
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,在四棱锥ABCD-PGFE中,底面ABCD是直角梯形,侧棱垂直于底面,AB//DC,∠ABC=45o,DC=1,AB=2,PA=1.
(1)求PD与BC所成角的大小;
(2)求证:BC⊥平面PAC;
(3)求二面角A-PC-D的大小。
正确答案
(1)取的AB中点H,连接DH,易证BH//CD,且BD=CD
所以四边形BHDC为平行四边形,所以BC//DH
所以∠PDH为PD与BC所成角
因为四边形,ABCD为直角梯形,且∠ABC=45o, 所以⊥DA⊥AB
又因为AB=2DC=2,所以AD=1,
因为Rt△PAD、Rt△DAH、Rt△PAH都为等腰直角三角形,
所以PD=DH=PH=
(2)连接CH,则四边形ADCH为矩形,
∴AH=DC 又AB=2,∴BH=1
在Rt△BHC中,∠ABC=45o ,
∴CH=BH=1,CB=
∴AD=CH=1,AC=
∴AC2+BC2=AB2
∴BC⊥AC
又PA平面ABCD
∴PA⊥BC ……7分
∵PA∩AC=A
∴BC⊥平面PAC
(3)
如图,分别以AD、AB、AP为x轴,y轴,z轴建立空间直角坐标系,则由题设可知:
A(0,0,0),P(0,0,1),C(1,1,0),D(1,0,0),
∴

设m=(a,b,c)为平面PAC的一个法向量,即
设

同理设n=(x,y,z) 为平面PCD的一个法向量,求得n=(1,1,1)
∴
所以二面角A-PC-D为60o
解析
解析已在路上飞奔,马上就到!
知识点
19.英语老师要求学生从星期一到星期四每天学习3个英语单词;每周五对一周内所学单词随机抽取若干个进行检测(一周所学的单词每个被抽到的可能性相同)
(1)英语老师随机抽了4个单词进行检测,求至少有3个是后两天学习过的单词的概率;
(2)某学生对后两天所学过的单词每个能默写对的概率为

正确答案
(1)设英语老师抽到的4个单词中,至少含有3个后两天学过的事件为A,则由题意可得
(2)由题意可得ξ可取0,1,2,3,则有P(ξ=0)
P(ξ=1)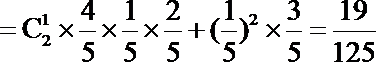
P(ξ=2) 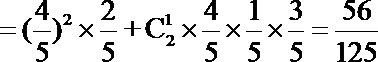
P(ξ=3)
所以ξ的分布列为:
故Eξ=0×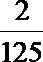
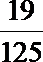
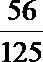
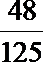
解析
解析已在路上飞奔,马上就到!
知识点
16.在△ABC中,角A、B、C所对的边分别为a、b、c, q=(



(1)求sin A的值;
(2)求三角函数式
正确答案
解:(1)∵

根据正弦定理,得
又



又
(2)原式

∵

∴
∴
∴

解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆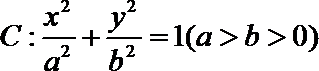

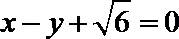
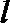
(1)求椭圆C的方程;
(2)求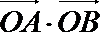
(3)若B点在于x轴的对称点是E,证明:直线AE与x轴相交于定点。
正确答案
(1)解:由题意知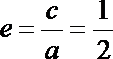
∴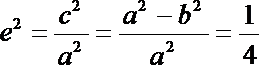
又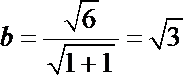
∴
故椭圆的方程为
(2)解:由题意知直线l的斜率存在,设直线l的方程为
由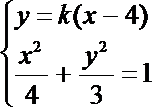
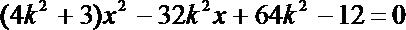
由
得:
设A(x1,y1),B (x2,y2),则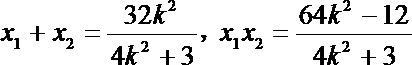
∴
解析
解析已在路上飞奔,马上就到!
知识点
21.(1)证明不等式:
(2)已知函数


(3)若关于x的不等式


正确答案
解:(1)令
则
∴g(x)在

(2)由
当x=0或



∴

∴a≥0,综上:
(3)由已知


当x>0时,易得
令

由(2)知:令a=2得:

∴
由(1)得:
当





当x=0时,b∈R,综上:
解析
解析已在路上飞奔,马上就到!