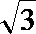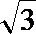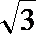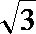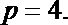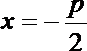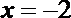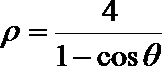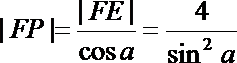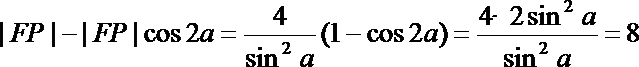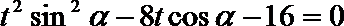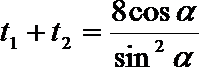- 真题试卷
- 模拟试卷
- 预测试卷
2.命题“若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知命题

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.下列命题中的假命题是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.点P从(1,0)出发,沿单位圆x2+y2=1按逆时针方向运动
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若直线的参数方程为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知命题


①命题“
②命题“
③命题“
④命题“
其中正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设集合A、B是全集


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 柱坐标(2,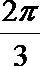
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.化极坐标方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设I是全集,I={0,1,2,3,4},集合A={0,l,2,3},集合B={4},则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 若P是极坐标方程为



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在直角坐标系中圆C的参数方程为




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知命题

正确答案
(0,1)
解析
解析已在路上飞奔,马上就到!
知识点
16.集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 在极坐标系中,已知两点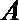
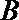
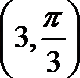
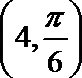
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
17. 已知直线l的参数方程为
(1)将曲线C的参数方程化为普通方程;
(2)若直线l与线C交于A、B两点,求线段AB的长.
正确答案
(1)
(2)将

设A,B对应的参数为



解析
解析已在路上飞奔,马上就到!
知识点
18.已知在直角坐标平面内,以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系,点


(1)求点
(2)若经过点


正确答案
(1)点

∵


化简得曲线C的直角坐标方程是
(2)设直线



代入
设其两根为

∴
当

解析
解析已在路上飞奔,马上就到!
知识点
21.已知集合

(1)若

(2)若
正确答案
(1)









即a=
(2)








解析
解析已在路上飞奔,马上就到!
知识点
19.已知曲线C的极坐标方程 是



(1)写出直线
(2)设曲线C经过伸缩变换




正确答案
(1)

(2)

设椭圆的参数方程
则
则
解析
解析已在路上飞奔,马上就到!
知识点
20.给定两个命题:
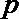


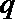
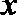
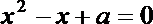
如果p
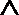
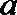
正确答案
对任意实数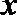
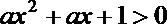

关于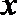


p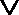

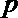
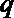
如果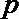

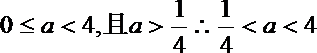
如果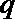
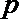

所以实数
解析
解析已在路上飞奔,马上就到!
知识点
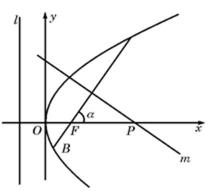
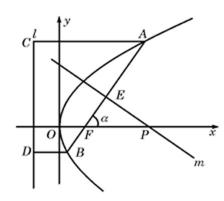
22.如图,倾斜角为α的直线经过抛物线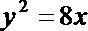
(1)求抛物线的焦点F的坐标及准线l的方程;
(2)若α为锐角,作线段AB的垂直平分线m交x轴于点P,证明|FP|-|FP|cos2α为定值,并求此定值
正确答案
(1)
解:设抛物线的标准方程为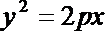

因此焦点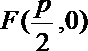
又准线方程的一般式为
从而所求准线l的方程为
(2)解法一:如图(21)图作AC⊥l,BD⊥l,垂足为C、D,以F点为极点,F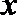
则由抛物线的定义 知抛物线方程为
则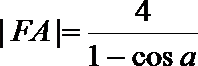
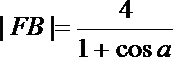
记直线m与AB的交点为E,则
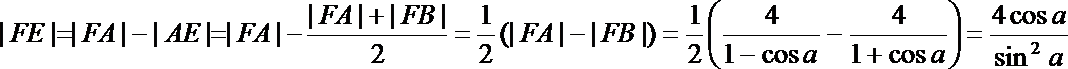
故
解法二:设直线AB: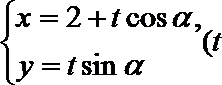
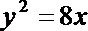
因为直线AB与抛物线有两个交点,因此上述方程有两个根,设两个根分别为 t1,t2,
则
所以|FE|=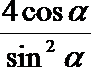
从而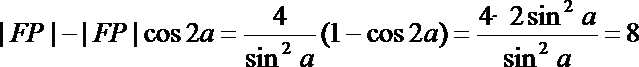
解法三:设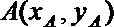
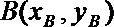
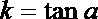
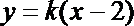
将此式代入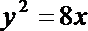
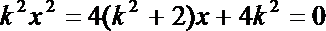
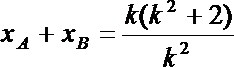
记直线m与AB的交点为
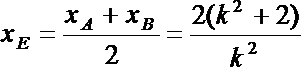
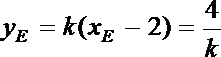
故直线m的方程为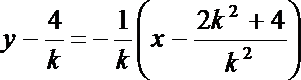
令y=0,得P的横坐标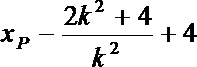
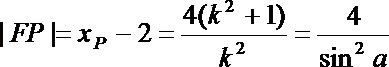
从而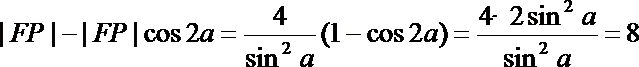
解析
解析已在路上飞奔,马上就到!