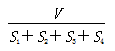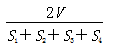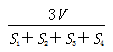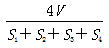- 真题试卷
- 模拟试卷
- 预测试卷
1.复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设△ABC的三边长分别为a、b、c,△ABC的面积为S,内切圆半径为r ,则r=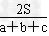
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.给出下列四个命题:
①在△ABC中,∠A>∠B是sinA>sinB的充要条件;
②给定命题


③设


④若直线


其中正确命题的序号是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 函数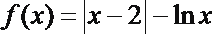
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8..已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.欧阳修《卖油翁》中写到:(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿. 可见 “行行出状元”,卖油翁的技艺让人叹为观止. 若铜钱是直径为3cm的圆,中间有边长为1cm的正方形孔,若随机向铜钱上滴一滴油(油滴的大小忽略不计),则油滴正好落入孔中的概率是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.△ABC的三个内角A、B、C所对的边分别为a,b,c,

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
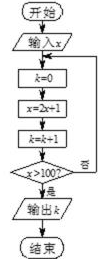
7.按如图所示的程序框图运算,若输入
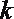
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数f(x)=ax2+bx-1(a,b∈R且a>0)有两个零点,其中一个零点在区间(1,2)内,则a-b的取值范围为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.下图是一个几何体的三视图,则该几何体的体积为_____.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.数列




正确答案
15
解析
解析已在路上飞奔,马上就到!
知识点
15.(考生注意:请在下列二题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(1)(几何证明)
选如图,A,E是半圆周上的两个三等分 点,直径BC=4,AD⊥BC,垂足为D,BE与AD相交于点F,则AF的长为___________.
(2)(坐标系与参数方程)
在已知极坐标系中,已知圆


正确答案
(1)
(2)2或-8
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.如图,已知直三棱柱ABC—A1B1C1,


(1)判断直线CF和平面AEB1的位置关系,并加以证明;
(2)求四棱锥A—ECBB1的体积.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知动点P





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.在直角坐标系













(1)求轨迹
(2)当



正确答案
(1)∵点



∴





(2)将


因为直线




设



且
显然,曲线




由

将②、③代入上式,整理得
所以


经检验,都符合条件①当


显然,此时直线



当


显然,此时直线


综上,




解析
解析已在路上飞奔,马上就到!
知识点
20.设数列






(1)当

(2)设





正确答案
(2)

得
注意到,当n为奇数时,


所以


对于任意的正整数n都有
所以


解析
解析已在路上飞奔,马上就到!
知识点
17. 已知函数
(1)求函数
(2)先将函数





正确答案
(1)因为
函数f(x)的最小正周期为

由

得f(x)的单调递增区间为

(2)根据条件得

当

所以当x = 

解析
解析已在路上飞奔,马上就到!
知识点
18.某校高三(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
(1)求全班人数及分数在

(2)若要从分数在

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数


(1)若


(2)求证:当


(3)若对任意的



正确答案
解:( 1)由已知,得 




(3)



于是问题等价于:对任意的

记

则










若


在此区间上,有 


这时,







解析
解析已在路上飞奔,马上就到!