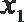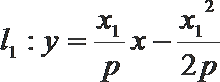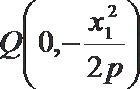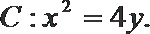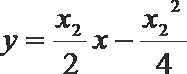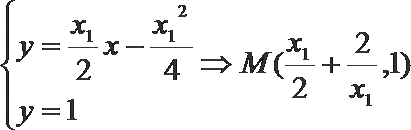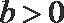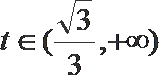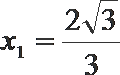- 真题试卷
- 模拟试卷
- 预测试卷
5.设甲:函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如图,在ΔABC中,



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.由1,2,3,4,5,6,7七个数字排列成7位数,则相邻数互质的排法种数有( )种
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知抛物线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.下列命题正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.在

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.如果函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.盒中装有5个零件,其中2个是使用过的,另外

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.如右图,如果执行右面的程序框图,输入正整数

正确答案
5040
解析
解析已在路上飞奔,马上就到!
知识点
16.底面边长为










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.定义在R上的函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知一个三棱锥的三视图如图2所示,其中俯视图是顶角为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知数列


(1) 求数列
(2) 令





正确答案
(1)由题

由累加法,当
代入

又

(2)

记函数
所以
则
所以
由于





由于,



综上所述:当



解析
解析已在路上飞奔,马上就到!
知识点
20. 如图,直三棱柱




(1)求证:

(2)若四棱锥

正确答案
(1)略
(2)如图建系
则


∴
设平面

由
得
∴
又平面
∴
∵所求二面角的平面角为锐角
∴二面角
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数
(1)若点




(2)设


(3)求函数
正确答案
(1)
(2)1
(3)
解析
解析已在路上飞奔,马上就到!
知识点
22.设

(1)若

(2)讨论

(3)是否存在




正确答案
(1)当


故
当





故

(2)
令


显然




故


故

注意到:当




①当





②当




综上:当



当


(3)假设存在








联立得:


令
则


(







即当





因为

故


由观察易得


综上可得:存在唯一的



解析
解析已在路上飞奔,马上就到!
知识点
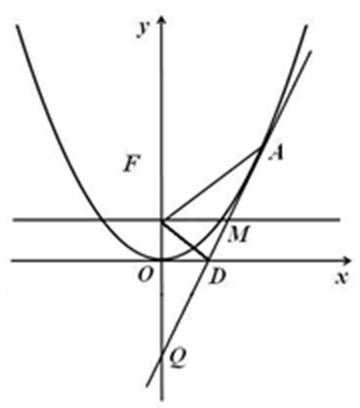
21.已知抛物线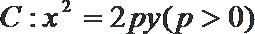
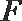
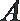
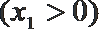
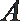

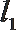
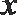
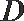
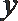
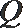
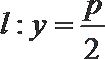
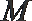
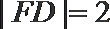
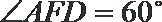
(1)求证: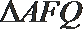

(2)若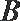
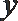



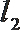
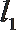
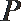
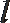
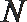
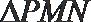
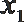
正确答案
(1)设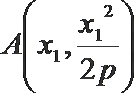
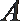
所以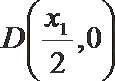
所以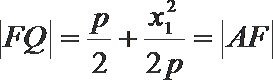
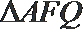
又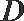
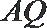

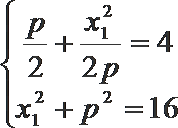
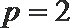
(2)设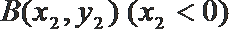
由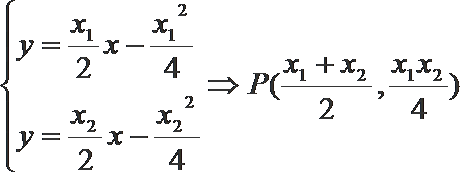
同理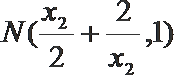
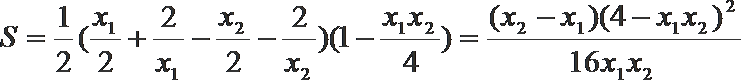
设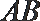
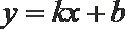
由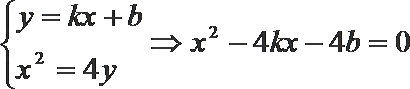
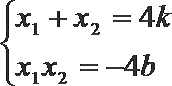
得: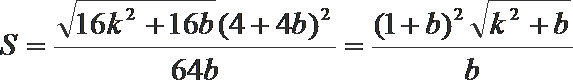
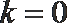
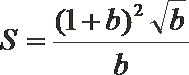
令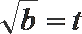
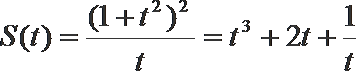
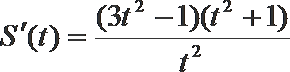
所以当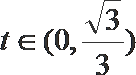
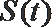
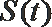
所以当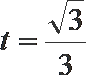
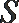
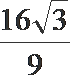
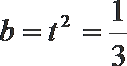
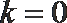
所以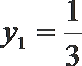
解析
解析已在路上飞奔,马上就到!