- 真题试卷
- 模拟试卷
- 预测试卷
2.对任意复数z=a+bi(a,b ∈R),i为虚数单位,则下列结论中正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.双曲线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.某学生在一门功课的22次考试中,所得分数如下茎叶图所示,则此学生该门功课考试分数的极差与中位数之和为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设函数f(x)=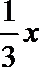
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.四面体ABCD中,AD与BC互相垂直,AD=2BC=4,且AB+BD=AC+CD=2
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.公差不为0的等差数列{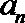
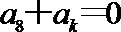
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在△ABC中,a,b,c分别是角A,B,C的对边,若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设全集U是实数集R,集合M={x|

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.在△ABC中,M是AB边所在直线上任意一点,若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.某几何体的三视图如图所示,则该几何体的表面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知函数f(x)是定义在R上的增函数,则函数y=f(|x-1|)-1的图象可能是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.圆

正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
14.不等式组
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.运行如下程序框图对应的程序,输出的结果是_______
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设数列{






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 为了整顿道路交通秩序,某地考虑将对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通行人中随机选取了200人进行调查,得到如下数据:
(Ⅰ)若用表中数据所得频率代替概率,则处罚10元时与处罚20元时,行人会闯红灯的概率的差是多少?
(Ⅱ)若从这5种处罚金额中随机抽取2种不同的金额进行处罚,在两个路口进行试验.
①求这两种金额之和不低于20元的概率;
②若用X表示这两种金额之和,求X的分布列和数学期望.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 已知函数f(x)=cos(2x-
(Ⅰ)求函数f(x)的最小正周期及其图象的对称轴方程;
(Ⅱ)设函数g(x)=[f(x)] 2+f(x),求g(x)的值域.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图所示的几何体ABCDFE中,△ABC,△DFE都是等边三角形,且所在平面平行,四边形BCED为正方形,且所在平面垂直于平面ABC.
(Ⅰ)证明:平面ADE∥平面BCF;
(Ⅱ)求二面角D-AE-F的正切值.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知圆C:




(Ⅰ)求椭圆E的方程;
(Ⅱ)求证:|AF|-|BF|=|BM|-|AM|.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请在第22~24三题中任选一题作答.
22.选修4—1:几何证明选讲如图,已知⊙O的半径为1,MN是⊙O的直径,过M点作⊙O的切线AM,C是AM的中点,AN交⊙O于B点,若四边形BCON是平行四边形;
(Ⅰ)求AM的长;
(Ⅱ)求
23.选修4—4:坐标系与参数方程
已知曲线C1的极坐标方程为ρcos(θ-


(Ⅰ)求曲线C2的直角坐标方程;
(Ⅱ)求曲线C2上的动点M到曲线C1的距离的最大值.
24.选修4—5:不等式选讲
已知不等式2|x-3|+|x-4|<2a.
(Ⅰ)若a=1,求不等式的解集;
(Ⅱ)若已知不等式的解集不是空集,求a的取值范围.
正确答案
22.
23.
24.
解析
解析已在路上飞奔,马上就到!
知识点
21. 对于函数f(x)(x∈D),若x∈D时,恒有


(Ⅰ)当函数f(x)=m
(Ⅱ)若函数g(x)为(0,+∞)上的J函数,
①试比较g(a)与
②求证:对于任意大于1的实数x1,x2,x3,…,xn,均有g(ln(x1+x2+…+xn))>g(lnx1)+g(lnx2)+…+g(lnxn).
正确答案
解析
解析已在路上飞奔,马上就到!













































