- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合A={x||x -

正确答案
解析
∵A=[-1,2],B=(0,4),则A∩B=(0,2].故选A.
知识点
3.已知函数f(x)=cos(2x-
正确答案
解析
依题意可得,2x+2a-



知识点
9.下图是某算法的程序框图,若程序运行后输出的结果是27,则判断框①处应填入的条件是( )
正确答案
解析
由框图的顺序,s=0,n=1,s=(s+n)n=(0+1)×1=1;n=2,依次循环s=(1+2)×2=6,n=3;注意此刻3>3仍然是“否”,所以还要循环一次s=(6+3)×3=27,n=4,此刻输出s=27.故选B.
知识点
5.从平行六面体的8个顶点中任取5个顶点为顶点,恰好构成四棱锥的概率为( )
正确答案
解析
四棱锥的底面可由6个侧面和6个对角面构成,每个底面对应4个四棱锥,故所求概率为P=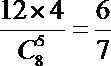
知识点
8.某几何体的三视图如图所示,当a+b取最大值时,这个几何体的体积为( )
正确答案
解析
由三视图知这个几何体是一个三棱锥P—ABC
其中PA⊥面ABC,AB=1,
PB=a,BC=b,PC=
设PA=x,AC=y,则
由
故三棱锥P—ABC的体积V=
故选D.
知识点
7.设直线x+y=1与抛物线y2=2px(p>0)交于A,B两点,若OA⊥OB,则△OAB的面积为( )
正确答案
解析
设A(x1,y1),B(x2,y2)
由x+y=1与抛物线y2=2px,得y2+2py-2p=0,
解得y1=-p+
y2=-p-

由OA⊥OB得,x1x2+y1y2=0
即[(1+p)2-(p2+2p)]+[p2-(p2+2p)]=0
化简得2p=1,
从而A(



OA2=x12+y12=5-2
△OAB的面积S=

故选B.
知识点
10.已知双曲线
正确答案
解析
点差得,



知识点
2.若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,那么复数
正确答案
解析
由图知,z=2+i,
∴
则对应的点位于复平面内的第四象限.
故选D.
知识点
4.设Sn为等差数列{an}的前n项和,若Sn=

正确答案
解析
∵Sn=na1+





∵故Sm+n-4=(m+n)a1+

知识点
6.设f(x)=(1+x)6(1-x)5,则导函数f ′(x)中x2的系数是( )
正确答案
解析
计算f′(x)中x2的系数较麻烦,只需计算f(x)中x3的系数.
f(x)=(1+x)(1-x2)5=(1-x2)5+x(1-x2)5,x3的系数为0-
故函数f′(x)中x2的系数是-15.故选D.
知识点
12.两球O1和O2在棱长为1的正方体ABCD—A1B1C1D1的内部,且互相外切,若球O1与过点A的正方体的三个面相切,球O2与过点C1的正方体的三个面相切,则球O1和O2的表面积之和的最小值为( )
正确答案
解析
∵AO1=

∴(

R1+R2=
球O1和O2的表面积之和为4π(R12+R22)≥4π ·2(

故选A.
知识点
11.函数f(x)=(x-a)ex在区间(2,3)内没有极值点,则实数a的取值范围是( )
正确答案
解析
f′(x)=(x+1-a)ex,依题意,x+1-a≥0或x+1-a≤0区间(2,3)内恒成立,
∴a≤3或a≥4.故选A.
知识点
21.已知函数f(x)=alnx+x2(a为实数).
(Ⅰ)求函数f(x)在区间[1,e]上的最小值及相应的x值;
(Ⅱ)若存在
正确答案
(Ⅰ)解:f(x)=alnx+x2的定义域为(0,+∞),f′(x)=

当x

若a≥-2,f′(x)在[1,e]上非负(仅当a=-2,x=-1时,f′(x)=0),
故f(x)在[1,e]上单调递增,此时f(x)min=f(1)=1;
若-2e2<a<-2,令f′(x)<0,解得1≤x<
令f′(x)>0,解得
∴f(x)min=f(

若a≤-2e2,f′(x)在[1,e]上非正(仅当a=-2e2,x=e时,f′(x)=0),
故f(x)在[1,e]上单调递减,此时f(x)min=f(e)=a+e2.
综上所述,得a≥-2时,f(x)min=1,相应的x=1;
当-2e2<a<-2时,f(x)min=

当a≤-2e2时,f(x)min=a+e2,相应的x=e.
(Ⅱ)解:不等式f(x)≤(a+2)x可化为a(x-lnx)≥x2-2x.
∵x
因而a≥

令g(x)=


当x
从而g′(x)≥0(仅当x=1时取等号),∴g(x)在[1,e]上是增函数,
故g(x)min=g(1)= -1,∴实数a的取值范围是[-1,+∞).
解析
解析已在路上飞奔,马上就到!
知识点
17.在△ABC中,a,b,c分别是角A、B、C的对边,且
(Ⅰ)求角B的大小;
(Ⅱ)若△ABC的面积S=
正确答案
(Ⅰ )解:
由
即2sinAcosB+sinA=0,
而sinA≠0,∴cosB=-

(Ⅱ)解:因S=


解法一:由余弦定理b2=a2+c2-2accosB,得b=
由cosC=

解得BD=
解法二:作AE平行于BC,并延长BD交AE于E,
在△ABE中,∠BAE=

又BE2=AB2+AE2-2AB·AEcosA,
即BE2=16+1-2×4×1×
BD=

解析
解析已在路上飞奔,马上就到!
知识点
20.如图,椭圆C:

(Ⅰ)求椭圆C的方程;
(Ⅱ)是否存在分别以AD,AC为弦的两个相外切的等圆?若存在,求出这两个圆的圆心坐标;若不存在,请说明理由.
正确答案
(Ⅰ)解:设左焦点F的坐标为(-c,0),其中c=
∵e=


∴A(0,


∴AB:

联立解得D点的坐标为(-

∵△ADC的面积为15,∴



解得c=3,∴a=5,b=4,∴椭圆C的方程为
(Ⅱ)由(Ⅰ)知,A点的坐标为(0,4),D点的坐标为(-
假设存在这样的两个圆M与圆N,其中AD是圆M的弦,AC是圆N的弦,
则点M在线段AD的垂直平分线上,点N在线段AC的垂直平分线y=0上.
当圆M和圆N是两个相外切的等圆时,一定有A,M,N在一条直线上,且AM=AN.
∴M、N关于点A对称,设M(x1,y1),则N(-x1,8-y1),
根据点N在直线y=0上,∴y1=8.∴M(x1,8),N(-x1,0),
而点M 在线段AD的垂直平分线y-



故存在这样的两个圆,且这两个圆的圆心坐标分别为
M(-

解析
解析已在路上飞奔,马上就到!
知识点
19.已知袋内有标有1~6数字的小球6个,球除标号不同外完全相同,甲、乙两人玩“摸球赢枣”的游戏,由丙做裁判,游戏规定由丙从袋中有放回的摸三次球,记第1、2、3次摸到的球的标号分别为a,b,c,然后将所得的数代入函数f(x)=ax2+bx+c,若所得到的函数无零点,则甲输一个枣给乙,若所得到的函数有零点,则乙输四个枣给甲.
(Ⅰ)记函数的零点的个数为,求的分布列和数学期望;
(Ⅱ)根据两人得枣的数学期望,该游戏公平吗?若不公平,谁吃亏?
正确答案
(Ⅰ)解:ξ的可能取值为0,1,2.f(x)=ax2+bx+c的判别式Δ=b2-4ac,
当Δ=0时,b为偶数,b=2时,a=1,c=1;
b=4时,a=1,c=4或a=2,c=2或a=4,c=1;
b=6时,a=3,c=3,∴P(ξ=1)=
当Δ≥0时,有b≥3,b=3时,ac≤2,有3种;
b=4时,ac≤4,有9种;b=5时,ac≤6,
有14种;b=6时,ac≤9,有17种,共计43种.
∴ξ=1的情形有43-5=38种,∴P(ξ=2)=
P(ξ=0)=1- P(ξ=1)-P(ξ=2)=
∴ξ的分布列为:
数学期望 Eξ=
(Ⅱ)甲得枣的数学期望是
乙得枣的数学期望是
∴该游戏不公平,甲吃亏.
解析
解析已在路上飞奔,马上就到!
知识点
22.请考生在下列三题中任选一题作答,如果多做,则按所做的第一题计分,做答时请写清题号.
1.设AB为圆O的直径,AB=10.E为线段AO上一点,OE=
2.设直线l的参数方程为


(Ⅰ)将曲线C的极坐标方程化为直角坐标方程,并指出曲线是什么曲线;
(Ⅱ)若直线l与曲线C交于A,B两点,求|AB|.
3.若实数a,b满足ab>0,且a2b=4,若a+b≥m恒成立.
(Ⅰ)求m的最大值;
(Ⅱ)若2|x-1|+|x|≤a+b对任意的a,b恒成立,求实数x的取值范围.
正确答案
1.
∵AB=10,OE=

CD=2


由相交弦定理知CE·ED=AE·EB=(




∴CE2+ED2=(CE+ED)2-2CE·ED=


2.
3.
(Ⅰ)解:由题设可得b=


当a=2,b=1时,a+b取得最小值3,∴m的最大值为3.
(Ⅱ)解:要使2|x-1|+|x|≤a+b对任意的a,b恒成立,须且只须2|x-1|+|x|≤3.
用零点区分法求得实数x的取值范围是-

解析
解析已在路上飞奔,马上就到!
知识点
16.关于x的不等式

正确答案
(
解析
∵
∴方程x2+ax+2b=0一根在[0,1)内,另一根在(1,2]内
即函数f(x)=x2+ax+2b的图象与x轴在[0,1)和(1,2]内各有一个交点.
∴
∵
由图可知,kPA<
∴kPA=


知识点
18.在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥面ABC,D、E分别是棱A1B1,AA1的中点,点F在棱AB上,且AF=
(Ⅰ)求证:EF∥平面BDC1;
(Ⅱ)求二面角E-BC1-D的余弦值.
正确答案
(Ⅰ)证明(证法一):设O为AB的中点,连结A1O,
∵AF=
又E为AA1的中点,∴EF∥A1O.
又∵D为A1B1的中点,O为AB的中点,∴A1D=OB.
又A1D∥OB,∴四边形A1DBO为平行四边形.
∴A1O∥BD.又EF∥A1O,∴EF∥BD.
又EF平面DBC1,BD平面DBC1.
∴EF∥平面DBC1.
(证法二)建立如图所示的坐标系.(坐标系建立仅为参考)
∵AB=BC=CA=AA1=2,D、E分别为A1B1、AA1的中点,
AF=
E(-1,0,1),F(-
C1(0,
设平面DBC1的法向量为n=(x,y,z).








令z=1,则y=0,x=2,∴n=(2,0,1).



又EF平面BDC1,∴EF∥平面BDC1.
(Ⅱ)解:设平面EBC1的法向量为m=(x,y,z).






令x=1,则z=2,y=-

cos< m,n >=
∴二面角E-BC1-D的余弦值为
解析
解析已在路上飞奔,马上就到!
知识点
13.6个儿童分坐两行,每行3人面对着做游戏,其中甲、乙二人既不对面,又不相邻的坐法有___________种。(用数字作答)
正确答案
384
解析
由于甲、乙是特殊元素,可先安排甲、乙,分两种情况:
(1)甲坐两端,可从四个位中选一个坐下,有



(2)甲在中间两个位上找一个位子坐下,有



所以满足条件的坐法共有
知识点
15.如果双曲线x2-y2=a2经过圆(x-3)2+(y-1)2=5的直径AB的两个端点,则正实数a的值等于___________。
正确答案
1+
解析
设A(x1,y1),B(x2,y2),代入双曲线方程作差得(x1+x2)(x1-x2)=(y1+y2)(y1-y2),
∵x1+x2=6,y1+y2=2,
∴(x-3) 2=
知识点
14.△ABC 外接圆的圆心为O,且
正确答案
解析
设BC边中点为M,则
由题设
∴A、O、M共线,且AO=4OM
而∠BOM=2∠BAM,∴∠BOM=∠BAC,
即cos∠BAC=
故填






































