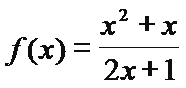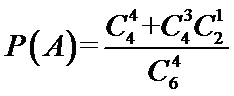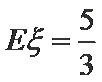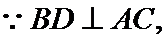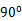- 真题试卷
- 模拟试卷
- 预测试卷
1.已知全集I=R,集合A={x|y=},集合B={x|0≤x≤2},则(∁IA)∪B等于( )
正确答案
解析
化简集合A={x|x
考查方向
解题思路
先化简集合A,然后求A 在I中的补集,最后求与B的并集.
易错点
化简集合A易出错,
知识点

6.由不等式组确定的平面区域记为Ω1,不等式组确定的平面区域为Ω2,在Ω1中随机取一点,则该点恰好在Ω2内的概率为( )
正确答案
解析
画出两个区域所表示的图形如图所示,




考查方向
解题思路
画出图形,算出面积,进而求出概率.
易错点
易错点是,容易把图形画错.
知识点
7.函数f(x)=sin(2x+φ)的图像向左平移

正确答案
解析
f(x)向右平移







考查方向
解题思路
先平移,然后根据图像关于原点对称求解φ,再利用函数的单调性求最小值
易错点
1、本题易在左右平移时发生错误,易忽视x的系数
知识点
8.设函数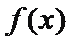
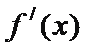

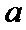



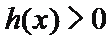

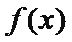
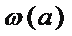
①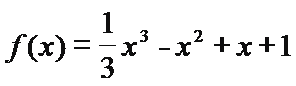
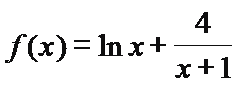
③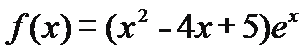
其中具有性质
正确答案
解析
①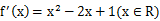
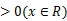
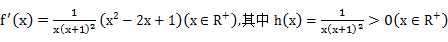
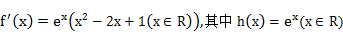
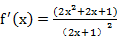
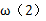
考查方向
解题思路
分别对函数求导,变形与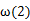
易错点
不理解函数新信息的性质而出错
知识点
2.设{an}是公比为q的等比数列,则“q>1”是“{an}为递增数列”的( )
正确答案
解析
根据指数函数的单调性,举反例:首项

考查方向
本题考查等比数列的单调性,充分条件与必要条件.
解题思路
等比数列的增减是由首项与公比确定的,当首项

易错点
对递增等比数列判断不准,对条件的性质判断不准.
知识点
3.根据如下样本数据

正确答案
解析
画出散点图,可知>0,<0 ,所以选B
考查方向
解题思路
画出散点图,可知>0,<0
易错点
不理解数据与回归直线的关系而出错
知识点
4.某几何体的三视图如图所示,则该几何体的体积为( )
正确答案
解析
v=
考查方向
解题思路
根据题中条件画出还原的几何体直观图,如图所示,是长方体与半个圆柱的组合体.
易错点
没有正确分析图中的位置关系与数量关系,将三视图还原错误.
知识点
5.执行右边的程序框图,若p=0.8,则输出的n=( )
正确答案
解析
根据程序逐步推理计算:p=0.8,n=1,s=0,0<0.8成立;s=s+









考查方向
解题思路
可以根据程序框图的运行方式,找出n的运算规律.
易错点
对循环结构的次数弄不清。对判断结构判断不准.
知识点
10.若偶函数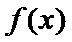
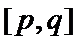
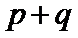
正确答案
0
解析
p+q=0
考查方向
解题思路
偶函数定义的特点是关于原点对称
易错点
没有掌握偶函数的定义的特点
知识点
9.已知复数z=(5+2i)2(i为虚数单位),则z的实部为________.
正确答案
21.
解析
先做乘法运算,z=25+20i-4=21+20i, 实部为21.
考查方向
解题思路
先做乘法运算,注意:
易错点
对复数的乘法运算不熟练,不理解复数的实部.
知识点
已知△ABC中,内角A,B,C的对边分别为a,b,c,且2cos2=sin B,b=1.
15.若A=,求边c;
16.若a=2c,求△ABC的面积.
正确答案
解析
解:由已知可得1+cos B=sin B…………2分
∴sin=.…………3分 又0
∴c=·sin C=.…………6分
考查方向
解题思路
先用二倍角公式降幂升角,然后再应用辅助角公式,求得角B、角C, 再由正弦定理解出c边长
易错点
三角恒等变换公式选择不准确,正余定理应用不熟练
正确答案
.
解析
解:由15题知B=,…………7分∴由余弦定理得b2=a2+c2-2accos B.……8分
又a=2c,∴c2=,…………10分∴△ABC的面积S=acsin B=.…………12分
考查方向
解题思路
根据第一问的角B的值, 得到a,c方程,又由a=2c,解出c,用 acsin B求面积。
易错点
三角恒等变换公式选择不准确,正余定理应用不熟练
如图所示,椭圆C1:+=1(a>b>0)的离心率为,x轴被曲线C2:y=x2-b截得的线段长等于C1的短轴长.C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A,B,直线MA,MB分别与C1相交于点D,E.
24.求C1,C2的方程
25.求证:MA⊥MB;
26. 记△MAB,△MDE的面积分别为S1,S2,若=λ,求λ的取值范围.
正确答案
C1的方程:+y2=1;C2的方程:y=x2-1
解析
由题意,知=,所以a2=2b2. ……1分
又2=2b,得b=1. ……2分
所以曲线C2的方程:y=x2-1,椭圆C1的方程:+y2=1. ……3分
考查方向
主要考查直线与圆锥曲线的综合应用能力,具体涉及到抛物线的方程,椭圆的方程,直线与圆锥曲线的相关知识. 本小题对考生的化归与转化思想、运算求解能力都有很高要求.
解题思路
根据题意直接列出a,b,c方程, 可求出两条曲线的方程
易错点
易在运算中出错,在转化直线与圆锥曲线关系过程中,易在切入点出错
正确答案
略
解析
证明 设直线AB:y=kx,A(x1,y1),B(x2,y2),由题意,知M(0,-1).
则⇒x2-kx-1=0, ……4分
则x1·x2=-1,x1+x2=k,

所以MA⊥MB. ……7分
考查方向
解题思路
设直线方程、交点坐标. 通过向量的数量积等于零, 证明两条线互相垂直
易错点
易在运算中出错,在转化直线与圆锥曲线关系过程中,易在切入点出错
正确答案
[,+∞)
解析
解: 设直线MA的方程:y=k1x-1,直线MB的方程:y=k2x-1,……8分
由25题知k1k2=-1,M(0,-1),
由解得或 ……9分
所以A(k1,k-1).同理,可得B(k2,k-1).……10分
故S1=|MA|·|MB|=·|k1||k2|.
由解得或
所以D(,).同理,可得E(,).……11分
故S2=|MD|·|ME|=·,
=λ==≥,……13分
则λ的取值范围是[,+∞).……14分
考查方向
主要考查直线与圆锥曲线的综合应用能力,具体涉及到抛物线的方程,椭圆的方程,直线与圆锥曲线的相关知识. 本小题对考生的化归与转化思想、运算求解能力都有很高要求.
解题思路
设MA,MB的方程,通过与抛物线,椭圆联立方程组,解出A,B,D,E的坐标,然后分别用



易错点
易在运算中出错,在转化直线与圆锥曲线关系过程中,易在切入点出错
设函数f(x)=ex-ax-2.
27.求f(x)的单调区间;
28.若a=1,k为整数,且当x>0时,(x-k)f′(x)+x+1>0恒成立,求k的最大值.
正确答案
当a≤0时,f(x)的单调递增区间为(-∞,+∞);当a>0时,f(x)的单调递减区间为(-∞,ln a),单调递增区间为(ln a,+∞)
解析
函数f(x)的定义域为(-∞,+∞),f′(x)=ex-a.……1分
当a≤0时,f′(x)>0,所以f(x)在区间(-∞,+∞)上单调递增;
……………………………………3分
当a>0时,若x∈(-∞,ln a),则f′(x)<0,若x∈(ln a,+∞),则f′(x)>0,
所以f(x)在区间(-∞,ln a)上单调递减,在区间(ln a,+∞)上单调递增.
……………………………………5分
综上可知,当a≤0时,f(x)的单调递增区间为(-∞,+∞);当a>0时,f(x)的单调递减区间为(-∞,ln a),单调递增区间为(ln a,+∞)……………………………………6分
考查方向
解题思路
先求导,根据导数的函数特点对,常数a进行合理讨论a小于等于零a大于零两种情况讨论
易错点
分类讨论不全,或者对含有参数的单调性讨论思路不清;
正确答案
k=2
解析
由于a=1,所以(x-k)f′(x)+x+1=(x-k)(ex-1)+x+1.
设g(x)=(x-k)(ex-1)+x+1,则g′(x)=ex(x-k+1).……………………………………7分
(i)若k≤1,则当x>0时,g′(x)>0,所以g(x)在区间(0,+∞)上单调递增,而g(0)=1,
故当x>0时,g(x)>1>0,即有(x-k)f′(x)+x+1>0恒成立.…………………………………9分
(ii)若k>1,则当x∈(0,k-1)时,g′(x)<0;当x∈(k-1,+∞)时,g′(x)>0.
所以g(x)在区间(0,+∞)内的最小值为g(k-1)=k-ek-1+1.………………………………11分
令h(k)=k-ek-1+1,则h′(k)=1-ek-1,因为k>1,所以h′(k)<0,故h(k)在区间(1,+∞)上单调递减.而h(2)>0,h(3)<0,所以当1<k≤2时,h(k)>0,即g(k-1)>0,从而当x>0时,g(x)>0,即(x-k)f′(x)+x+1>0恒成立;当k≥3时,h(k)<0,即g(k-1)<0,故g(x)>0在区间(0,+∞)内不恒成立.……………………………………13分
综上所述,整数k的最大值为2……………………………………14分
考查方向
解题思路
将a=1及导数代入得,g(x)=(x-k)(ex-1)+x+1,则g′(x)=ex(x-k+1).设


易错点
处理逻辑推理与运算求解能力方面易出错。思路不清晰,步骤不严谨
11.已知函数


正确答案
2.
解析
因为 


考查方向
解题思路
根据函数与反函数的关系可知,因为 


易错点
不理解函数与反函数的关系而出错.
知识点
12.从编号为0,1,2,…,79的80件产品中,采用系统抽样的方法抽取容量为5的一个样本,若编号为42的产品在样本中,则该样本中产品的最小编号为
正确答案
10.
解析
采用系统抽样的方法抽取容量为5的一个样本,应该将80件产品分成5组,每组16件产品,编号为42的产品在样本中,第三组的编号应该为31到48,所以是42号产品应该排在第三组中的第十位,所以第一组中最小的编号应该为10.所以本题填10.
考查方向
解题思路
采用系统抽样的方法是先分组,N

易错点
不理解系统抽样的编号原则问题出错.
知识点
13.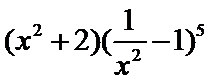
正确答案
3.
解析
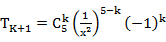
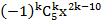
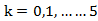
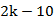
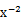
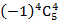
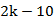
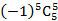
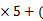
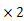
考查方向
解题思路
根据题意,要想找出展开式中的常数项,应通过通项,求第二个二项式展开式中的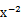
易错点
扩展形式的展开式中的常数项的确定方法掌握不清,容易丢项.
知识点
14.设点




正确答案
[-1,1]
解析
作OA⊥MN,垂足为A,在直角三角形OMA中,因为∠OMN=






考查方向
本题是2014年全国2卷理科第16小题,本小题主要考查直线与圆的位置关系,考查数形结合能力和逻辑思维能力,考查分析问题和解决问题能力
解题思路
如图,由题意可知直线MN与圆O有公共点即可,圆形O到直线MN的距离小于等于1即可.
易错点
找不到处理该问题的一个合理方法,找不到角度与坐标之间的关系
知识点
某企业招聘工作人员,设置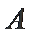

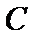
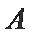
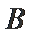

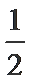
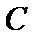
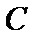
17.求戊竞聘成功的概率;
18.求参加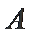
19.记

正确答案
解析
设戊竞聘成功为A事件,则 …………1分
考查方向
解题思路
至少答对3题有两种情况
易错点
事件的性质划分不清,随机变量的取值及相应概率求不准.
正确答案
解析
设“参加
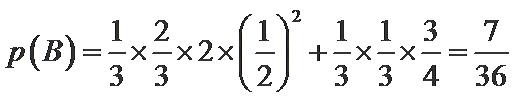
考查方向
解题思路
能出现参加A组测试通过的人数多余参加B组测试通过的人数有两种情况1>0或2>1;
易错点
事件的性质划分不清,随机变量的取值及相应概率求不准.
正确答案
解析
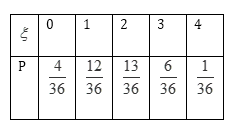
(Ⅲ)
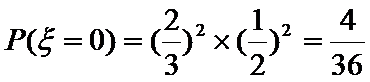
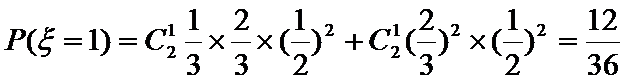


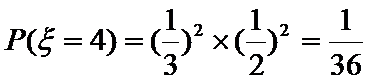
…………12分
∴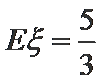
解题思路
根据题意,先确定随机变量可能取值为0,1,2,3,4,然后根据题意,分别求出相应的概率,得到分布列,由分布列求数学期望.
易错点
事件的性质划分不清,随机变量的取值及相应概率求不准.
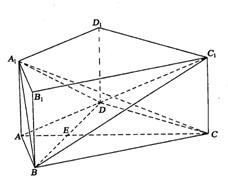
如图, 在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,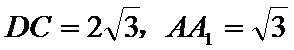
AD⊥DC,AC⊥BD, 垂足为E
20.求证:BD⊥A1C;
21.求二面角A 1-BD-C 1的大小;
正确答案
略
解析
在直四棱柱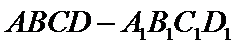
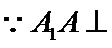
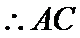

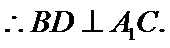
考查方向
解题思路
要证BD⊥A1C,可以寻找三垂线定理模型。
易错点
对垂直的论证不充分,不能充分应用图形的特点建系,在应用向量解决二面角问题时,思路不清晰。
正确答案
解析
连结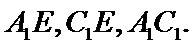
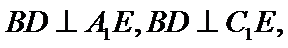

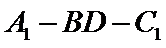
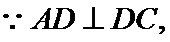
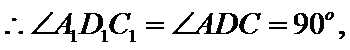
又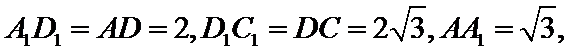
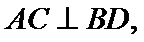
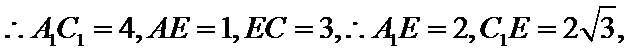
在
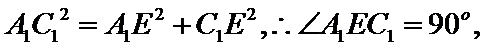
即二面角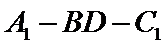

考查方向
解题思路
方法一:可以直接论证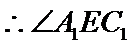

易错点
对垂直的论证不充分,不能充分应用图形的特点建系,在应用向量解决二面角问题时,思路不清晰。
已知正项数列




22.求

23.是否存在非零整数
对一切

正确答案

解析
解:由.
当



当
由
∵


∴

另法:易得



考查方向
解题思路
利用数列前


另法:易得



易错点
利用数列前


正确答案
存在
解析
由

设


∵


假设存在这样的实数


① 当

② 当


综上,


考查方向
解题思路
先进行化简转化




易错点
利用数列前