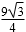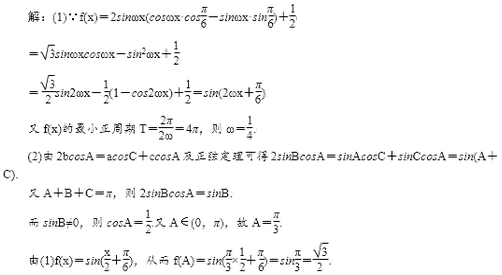- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合A={-2,0,1},集合B={x||x|<a且x∈Z},则满足A
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.形如45132这样的数称为“波浪数”,即十位数字,千位数字均比它们各自相邻的数字大,则由1、2、3、4、5可构成的数字不重复的五位“波浪数”的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若(1-2x)4=a0+a1x+a2x2+a3x3+a4x4,则|a0|+|a1|+|a2|+|a3|+|a4|的值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.如图,设D是图中边长分别为2和4的矩形区域,E是D内位于函数y=x2图象下方的区域(阴影部分),向D内随机抛掷30个点,则落在E内的点的个数约为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知命题p:“a=1是x>0,x+≥2的充分必要条件”,命题q:“x0∈R,x+x0-2>0”,则下列命题正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知cos(


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知函数f(x)=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知实数x,y满足线性约束条件
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.幂函数f(x)=xα(α为常数)的图象经过(3,

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.函数f(x)=exlnx-1的零点个数是
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
11.按下图所示的程序框图运算:若输出k=2,则输入x的取值范围是
正确答案
(28,57]
解析
解析已在路上飞奔,马上就到!
知识点
12.数列{an}满足:

正确答案
-1
解析
解析已在路上飞奔,马上就到!
知识点
13.已知函数f(x)=|x-2|,若a≠0,且a,b∈R,都有不等式

正确答案
[0,4]
解析
解析已在路上飞奔,马上就到!
知识点
14.在△ABC中有如下结论:“若点M为△ABC的重心,则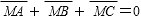
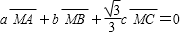


正确答案
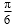
解析
解析已在路上飞奔,马上就到!
知识点
15.给定集合


正确答案
5 ;2m - 3
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数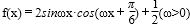
(1)求正实数ω的值;
(2)在△ABC中,内角A、B、C的对边分别为a、b、c,且满足2bcosA=acosC+ccosA,求f(A)的值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.若盒中装有同一型号的灯泡共12只,其中有9只合格品,3只次品。
(1)某工人师傅有放回地连续从该盒中取灯泡3次,每次取一只灯泡,求2次取到次品的概率;
(2)某工人师傅用该盒中的灯泡去更换会议室的一只已坏灯泡,每次从中取一灯泡,若是正品则用它更换已坏灯泡,若是次品则将其报废(不再放回原盒中),求成功更换会议室的已坏灯泡前取出的次品灯泡只数X的分布列和数学期望。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知数列{an}的前三项与数列{bn}的前三项对应相等,且
(1)求数列{an}与{bn}的通项公式;
(2)是否存在k∈N*,使得bk-ak∈(0,1)?请说明理由。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.某化工厂生产某种产品,每件产品的生产成本是3元,根据市场调查,预计每件产品的出厂价为x元(7≤x≤10)时,一年的产量为(11-x)2万件;若该企业所生产的产品全部销售,则称该企业正常生产;但为了保护环境,用于污染治理的费用与产量成正比,比例系数为常数a(1≤a≤3)。
(1)求该企业正常生产一年的利润L(x)与出厂价x的函数关系式;
(2)当每件产品的出厂价定为多少元时,企业一年的利润最大,并求最大利润。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.设函数y=f(x)的定义域为(0,+∞),且在(0,+∞)上单调递增,若对任意x,y∈(0,+∞)都有:f(xy)=f(x)+f(y)成立,数列{an}满足:a1=f(1)+1,

(1)求数列{an}的通项公式,并求Sn关于n的表达式;
(2)设函数g(x)对任意x、y都有:g(x+y)=g(x)+g(y)+2xy,若g(1)=1,正项数列{bn}满足:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.定义F(x,y)=(1+x)y,其中x,y∈(0,+∞)。
(1)令函数
(2)令函数
(3)当x,y∈N*,且x<y时,求证:
正确答案
解析
解析已在路上飞奔,马上就到!