- 真题试卷
- 模拟试卷
- 预测试卷
2.设a,b是实数,若=a+bi(i是虚数单位),则a+b的值是( )
正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
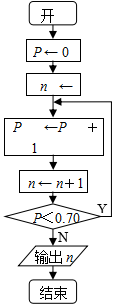
6.如图所示的流程图,最后输出的n的值是( )
正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
10.在平面直角坐标系xOy中, 抛物线方程为x2=2py(p>0)。 若直线x-y-2=0与该抛物线相切,则实数p的值是( )
正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合A={x|x2-2x≥0},B={-1, 0, 1, 2, 3},则A∩B= ( )
正确答案
{-1,0,2,3}
解析
解析已在路上飞奔,马上就到!
知识点
3.“|x|≤3”是“x≥-3且x≤3”的( )条件。(从 “充分不必要”、“必要不充分”、“充要”和“既不充分也不必要”中选填)
正确答案
充要
解析
解析已在路上飞奔,马上就到!
知识点
4.一只口袋装有形状、大小都相同的5只小球,其中2只白球,3只红球。从中一次随机摸出2只球,则2只球不同色的概率是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.为了解某地区高三学生的身体发育情况,抽查了该地区100名高三男生的体重。根据抽样测量后的男生体重(单位:kg)数据绘制的频率分布直方图如图所示,则这100名学生中体重值在区间[56.5,64.5)的人数是( )
正确答案
40
解析
解析已在路上飞奔,马上就到!
知识点
8.在平面直角坐标系xOy中,已知双曲线C:

正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
9.已知正方体的外接球的体积是
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知向量a,b,满足|a|=1,| b |=

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.设函数f(x)的定义域为D,
①y=x3 (x∈R);
②y=
③y=lnx (x∈(0,+∞));
④y=2sinx+1 (x∈R)。
上述四个函数中,满足所在定义域上“均值”为1的函数是( )(填满足要求的所有的函数的序号)
正确答案
①③④
解析
解析已在路上飞奔,马上就到!
知识点
14.设实数a,x,y,满足
正确答案

解析
解析已在路上飞奔,马上就到!
知识点
11.已知锐角A,B满足tan(A+B)=2tanA,则tanB的最大值是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设等比数列{an}的前n项和为Sn (n∈N*)。若S3,S9,S6成等差数列,则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 设△ABC三个内角A、B、C所对的边分别为a,b,c。已知C=
(1)求角A的大小;

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 如图,在四棱锥P-ABCD中,BA

(1)求证:AE//平面PBC;
(2)求证:平面PBC
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 交管部门遵循公交优先的原则,在某路段开设了一条仅供车身长为10m的公共汽车行驶的专用车道。据交管部门收集的大量数据分析发现,该车道上行驶着的前、后两辆公共汽车间的安全距离d(m)与车速v(km/h)之间满足二次函数关系d=f(v)。现已知车速为15 km/h时,安全距离为8 m;车速为45 km/h时,安全距离为38 m;出现堵车状况时,两车安全距离为2 m 。
(1)试确定d关于v的函数关系d=f(v);
(2)车速v(km/h)为多少时,单位时段内通过这条车道的公共汽车数量最多,最多是多少辆?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. (1)已知一条直线l与函数y=sinx(x∈R)的图象相切,且有无穷多个切点。试写出这条直线的方程,并说明理由。
(2)是否存在函数y=f(x)满足它的图象上任意两点处的切线都不相同?若存在,请举例说明;若不存在,请说明理由。
(3)设函数g(x)=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 设k为正整数,若数列{an}满足a1=1,且 (an+1-an)2=(n+1)k(n∈N*),称数列{an}为“k次方数列”。
(1)设数列{an}(n∈N*)为“2次方数列”,且数列
(2)设数列{an}(n∈N*)为“4次方数列”,且存在正整数m满足am=15,求m的最小值;
(3)对于任意正整数c,是否存在“4次方数列”{an}(n∈N*)和正整数p,满足ap=c 。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.【选做题】
在A、B、C、D四小题中只能选做2题。解答应写出文字说明、证明过程或演算步骤。
A.几何证明选讲
在△ABC中,已知AC=

B.矩阵与变换
在平面直角坐标系


C.坐标系与参数方程
在平面直角坐标系




D.不等式选讲
设

正确答案
A.
B.
C.
D.
解析
解析已在路上飞奔,马上就到!
知识点
22.如图,在三棱柱ABC-A1B1C1中,BA⊥AC,AB=AC=A1B=2,顶点A1在底面ABC上的射影恰为点B 。
(1)求异面直线AA1与BC所成角的大小;


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23. 设a为实数,若数列{an}的首项为a,且满足an+1=an2+a1(n∈N*),称数列{an}为理想数列。若首项为a的理想数列满足:对于任意的正整数n≥2,都有|an|≤2,称实数a为伴侣数。记M是所有伴侣数构成的集合。
(1)若a∈(-∞,-2),求证:
(2)若a∈(0,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 在平面直角坐标系xOy中,椭圆C:

(1)求a,b的值。
(2)设P是椭圆C长轴上的一个动点,过点P作斜率为k的直线l交椭圆C于A、B两点。
(ⅰ)若k=1,求△OAB面积的最大值;
(ⅱ)若PA2+PB2的值与点P的位置无关,求k的值。
正确答案
解析
解析已在路上飞奔,马上就到!