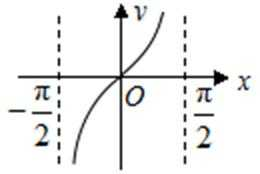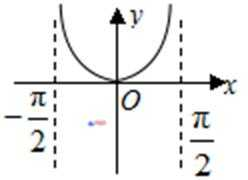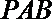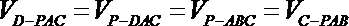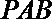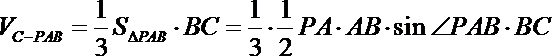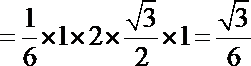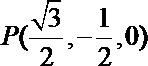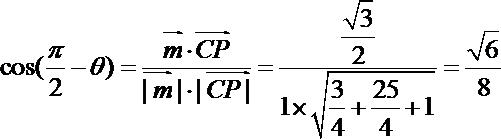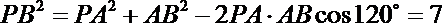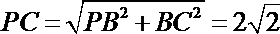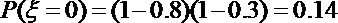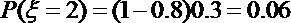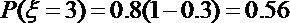- 真题试卷
- 模拟试卷
- 预测试卷
1.若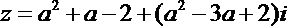
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.在三棱锥

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知正项数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.要得到函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
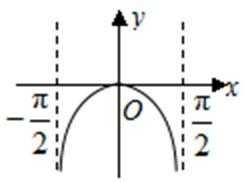
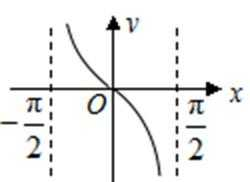
5.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知点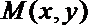
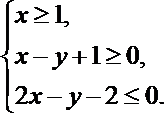
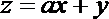
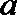
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 已知向量





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.函数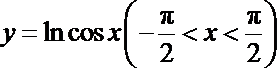
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.二项式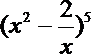
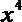
正确答案
40
解析
解析已在路上飞奔,马上就到!
知识点
13.设直线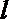
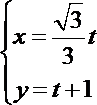
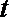
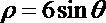
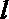
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.命题“
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.如图所示的程序框图,若
正确答案
32
解析
解析已在路上飞奔,马上就到!
知识点
14.已知集合
①若

②若

③若

④若


其中所有正确命题的序号是______________。
正确答案
②③
解析
解析已在路上飞奔,马上就到!
知识点
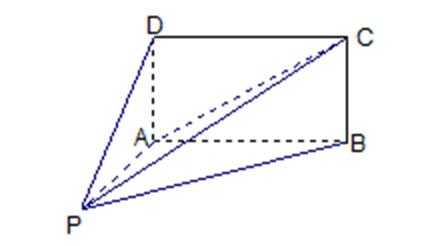
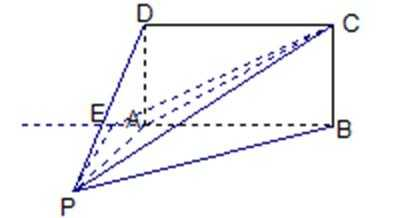
17.如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2, 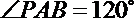
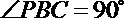
(1)求证:平面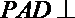
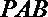
(2)求三棱锥D-PAC的体积;
(3)求直线PC与平面ABCD所成角的正弦值.
正确答案
(1)证明:∵ABCD为矩形
∴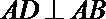
∵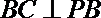
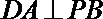
∴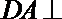
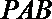
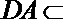
∴平面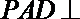
(2) ∵
由(1)知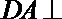
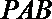
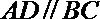
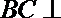
∴
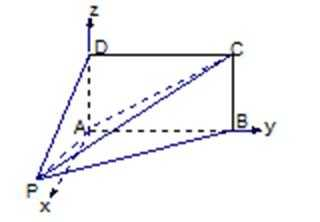
(3)解法1:
以点A为坐标原点,AB所在的直线为y轴建立空间直角坐标系如图示
则依题意可得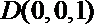
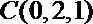
可得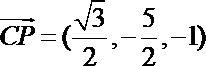
平面ABCD的单位法向量为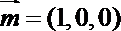
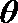
则
∴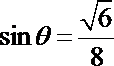
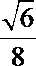
解法2:
由(1)知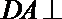
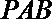
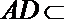
∴平面ABCD⊥平面PAB, 在平面PAB内,过点P作PE⊥AB,垂足为E,
则PE⊥平面ABCD,连结EC,则∠PCE为直线PC与平面ABCD所成的角
在Rt△PEA中,∵∠PAE=60°,PA=1
∴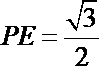
∴
在Rt△PEC中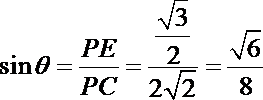
即直线PC与平面ABCD所成角的正弦值
解析
解析已在路上飞奔,马上就到!
知识点
19.某校教务处要对高三上学期期中数学试卷进行调研,考察试卷中某道填空题的得分情况.已知该题有两空,第一空答对得3分,答错或不答得0分;第二空答对得2分,答错或不答得0分.第一空答对与否与第二空答对与否是相互独立的.从该校1468份试卷中随机抽取1000份试卷,其中该题的得分组成容量为1000的样本,统计结果如下表:
(Ⅰ)求样本试卷中该题的平均分,并据此估计该校高三学生该题的平均分.
(Ⅱ)该校的一名高三学生因故未参加考试,如果这名学生参加考试,以样本中各种得分情况的频率(精确到0.1)作为该同学相应的各种得分情况的概率.试求该同学这道题得分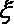
正确答案
解:(Ⅰ)设样本试卷中该题的平均分为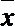
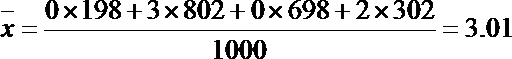
据此可估计该校高三学生该题的平均分为3.01分.
(Ⅱ)依题意,第一空答对的概率为0.8,第二空答对的概率为0.3,
则该同学这道题得分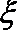
所以E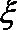
解析
解析已在路上飞奔,马上就到!
知识点
20.设数列



(1)求证:数列
(2)若


(3)在(2)的条件下,设数列


正确答案
(1)解:∵

当n≥2时,
①-②得:

进而
③-④得
所以数列
(2)解:由(1)知数列

∵
∴当n = 1时,

由⑤-⑥得:


故
(3)解:


⑦-⑧并化简得:
所以
因为
所以

∴
所以
所以
解析
解析已在路上飞奔,马上就到!
知识点
21.已知:向量

(1)求动点 M 的轨迹 C 的方程;
(2)已知直线







正确答案
解:设点
∵
∴
∴点 M 的轨迹C是以
∴
∴ 动点M 的轨迹 C的方程为
(2)
由(1)知,轨迹C是椭圆

设满足条件的直线



则直线

将①代入椭圆方程并整理得:


将②代入椭圆方程并整理得:

由△BDE是等腰直角三角形得
∴

∵方程④

∴即满足条件的直线

解析
解析已在路上飞奔,马上就到!
知识点
16.锐角三角形ABC的三内角A、B、C所对边的长分别为


(1)求角B的大小;
(2)若

正确答案
解:(1)

即
(2)


解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数


(1)求实数
(2)求

正确答案
解:(1)当
∴
依题意

又
∴
(2)当





当x变化时,





∴当

当
若


若


当


∵当

当

∴
解析
解析已在路上飞奔,马上就到!