- 真题试卷
- 模拟试卷
- 预测试卷
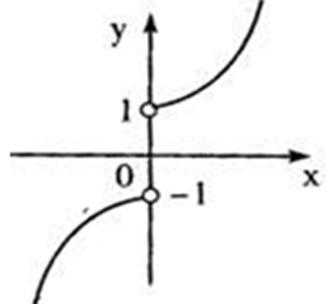
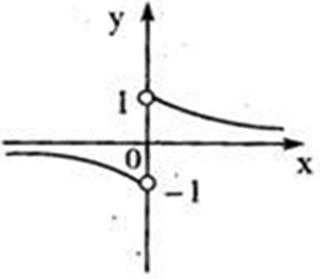
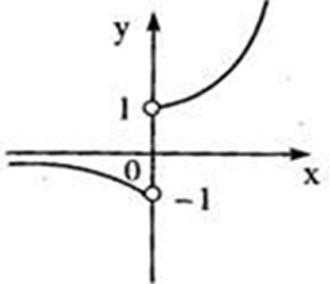
1.若集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 当

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数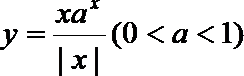
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知定义在R上的偶函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.若定义运算


正确答案
(0,1]
解析
解析已在路上飞奔,马上就到!
知识点
16.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数

正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
13.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.函数

正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
15.定义区间





正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
18.已知命题P:函数




正确答案
解:∵命题P:函数
∴
又∵命题Q:不等式

∴
或
即:
∵

解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数

(1) 求函数
(2) 当


(3) 若对任意


正确答案
解:(1) 由
解得:





(2) 设


则
∴

∴

∴

(3) 对任意

即:

∴ 


∴
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1) 求
(2) 设



正确答案
解:(1) ∵ 函数
∴

∴ 
(2) 
函数

方程
由已知得:
∴
方程等价于:
设

若


∴ 
若

若



当

当

综上所述:实数
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数

(1)如果函数


(2)是否存在实数



正确答案
解:(1) 当


当


由于

所以



当


(2)把方程

即为方程


原方程在区间(
即为函数

令



当


当






解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数.
(1) 求函数的定义域,并求
(2) 若


正确答案
解:(1) 由

∴函数
∵
∴
∴
(若直接代入计算也给分)
(2) ∵

∴

∴
解析
解析已在路上飞奔,马上就到!