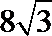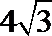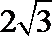- 真题试卷
- 模拟试卷
- 预测试卷
1.设全集

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
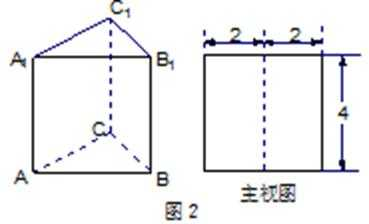
3.如图2,正三棱柱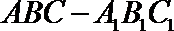
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.设函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若
①存在一条直线

②存在一个平面

③存在两条平行直线


④存在两条异面直线


那么可以是

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若三棱锥







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若变量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.如图,在等腰直角









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 将甲、乙、丙、丁、戊共五位同学分别保送到北大、上海交大和浙大3所大学,若每所大学至少保送1人,且甲不能被保送到北大,则不同的保送方案共有( )种.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.定义域为








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在
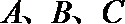
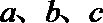
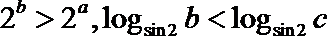
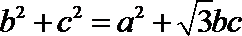
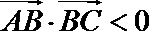
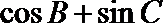
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.圆






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图所示,正方形




(1)求证:
(2)求证:
(3)在线段




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为
(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为

下面的临界值表供参考:
(参考公式:

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知










(1)求曲线
(2)设曲线




(3)在(1)、(2)的条件下,直线








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数

(1)求实数
(2)若关于



(3)证明:对任意的正整数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.根据如图的程序框图,将输出的


(1)写出数列
(2)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
选做题:请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题计分.
22.选修4—1:几何证明选讲
如图,已知









求证:
(1)
(2)
23.选修4—4:坐标系与参数方程
在直角坐标系







(1)若直线


(2)设


24.选修4—5:不等式选讲
设函数
(1)当
(2)若


正确答案
22.

23.

24.
解析
解析已在路上飞奔,马上就到!