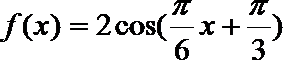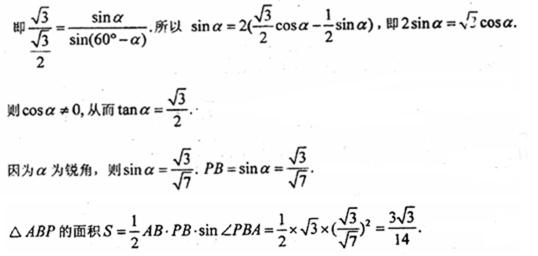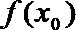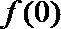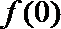- 真题试卷
- 模拟试卷
- 预测试卷
2. 命题“和为偶数的两个整数都为偶数”的否定是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 已知二次函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.由直线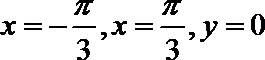
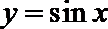
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.以



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若复数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 在






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.“


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.在数列











正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知平面向量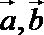
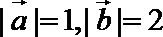
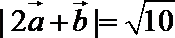
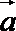
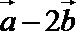
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.定义全集






①若



②对于任意

③对于任意

④对于任意

其中正确的结论有_______.(写出全部正确结论的序号)
正确答案
①②③
解析
解析已在路上飞奔,马上就到!
知识点
11.在极坐标系中,点

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.把函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
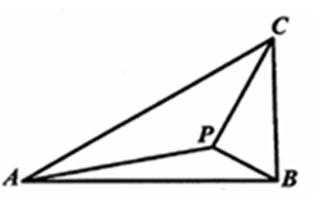
16.已知函数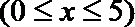
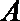
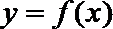
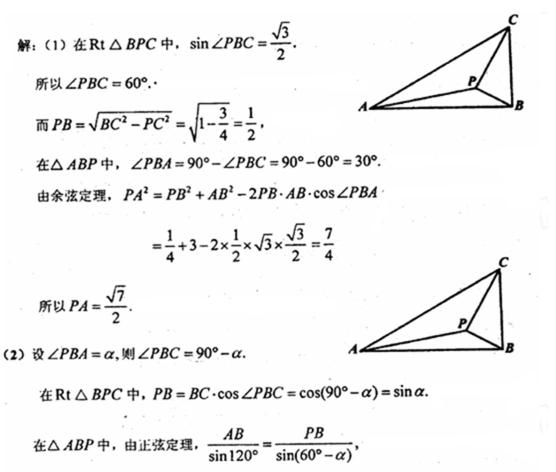
(1)求点
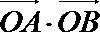
(2)设点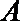
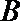
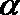
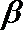
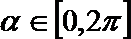
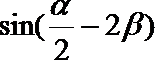
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(1)若


(2) 在(1)的结论下,设函数
(3)设函数


















正确答案
解:(1)依题意:
∵
∴
∴

∴b的取值范围为
(2)设

∴当
当
当
综上所述,当
当
(3)设点P、Q的坐标是
则点M、N的横坐标为
C1在M处的切线斜率为
C2在点N处的切线斜率
假设C1在点M处的切线与C2在点N处的切线平行,则
即
则


设
令
则
∵
∴
所以
故

这与①矛盾,假设不成立,
故C1在点M处的切线与C2在点N处的切线不平行.
解析
解析已在路上飞奔,马上就到!
知识点
18.设公差不为
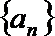
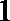
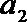
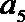
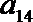
(1)求数列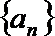
(2)若数列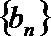
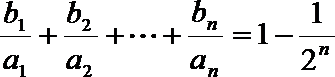
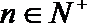
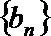

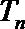
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.现有六名篮球运动员进行传球训练,由甲开始传球(第一次传球是由甲传向其他五名运动员中的一位),若第

(1)求出




(2)证明数列

(3)当


正确答案
解.(1)

第


∴当

(2)由



又



从而

(3).当



当


综上,当


解析
解析已在路上飞奔,马上就到!
知识点
17.在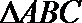
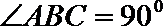
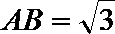
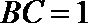
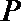
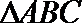
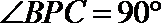
(1)若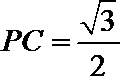
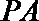
(2)若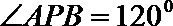
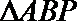
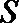
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.对于定义域为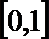
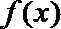
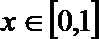
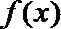

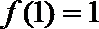
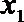

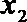

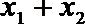
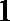
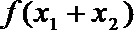
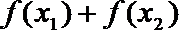
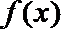
(1)若函数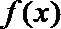
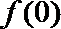
(2)判断函数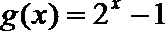
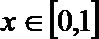
(3)若函数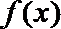
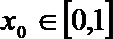
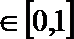
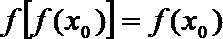
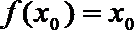
正确答案
解:(1)取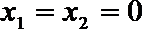
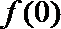
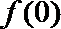
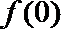

又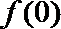

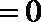
(2)当
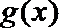

又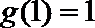
若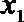

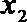

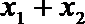
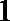
则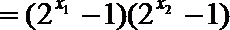

故函数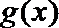
(3)由条件③,任给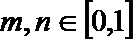
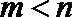
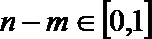
且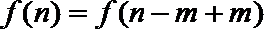
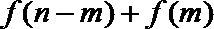
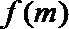
若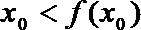
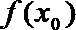
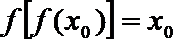
若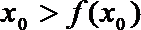
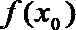
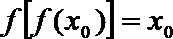
故
解析
解析已在路上飞奔,马上就到!