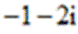- 真题试卷
- 模拟试卷
- 预测试卷
1．已知全集
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2．已知
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．设{an}是有正数组成的等比数列，
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．已知圆的方程x2＋y2＝4，若抛物线过点A(0，－1)，B(0,1)且以圆的切线为准线，则抛物线的焦点轨迹方程是( )
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．用数字2,3,5,6,7组成没有重复数字的五位数，使得每个五位数中的相邻的两个数都互质，则得到这样的五位数的概率为（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．在△ABC中，内角A,B,C的对边分别是a,b,c，若
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．下面给出的四个点中，到直线x－y＋1＝0的距离为
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．已知直线x＋y＋m＝0与圆x2＋y2＝2交于不同的两点A、B，O是坐标原点，
A
B(－2,2)
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．已知以T = 4为周期的函数
A（
B（
C（
D（
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13．已知函数y＝asin2x＋bcos2x＋2(ab≠0)的一条对称轴方程为
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．设复数满足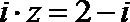
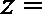
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17.如图，四边形OABC是边长为1的正方形，OD＝3，点P为△BCD内（含边界）的动点，设
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14．某少数民族的刺绣有着悠久的历史,下图（1）、（2）、（3）、（4）为她们刺绣最简单的四个图案,这些图案都是由小正方形构成，小正方形数越多刺绣越漂亮;现按同样的规律刺绣（小正方形的摆放规律相同），设第
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15．已知函数f(x)是定义在R上的偶函数，定义在R上的奇函数g(x)过点(－1,1)，且g(x)＝f(x－1)，则f(7)＋f(8)的值为______．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．设
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16．在Rt△ABC中 ，AB＝AC＝1，以点C为一个焦点作一个椭圆，使这个椭圆的另一个焦点在AB边上，且这个椭圆过A、B两点，则这个椭圆的焦距长为（ ）．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
19．有两辆汽车由南向北驶入四叉路口，各车向左转，向右转或向前行驶的概率相等，且各车的驾驶员相互不认识.
（I）规定：“第一辆车向左转，第二辆车向右转”这一基本事件用“（左，右）”表示。又“(直，左)”表示的是基本事件：“第
（II）求至少有一辆汽车向左转的概率；
（III）设有
正确答案
（I） (左，左)；(左，直)；(左，右)；(直，右)；(直，左)；(直，直)；（右，右)；(右，直)；(右，左)
基本事件共有9种.
（II）至少有一辆汽车向左转的事件数有5种，
所求概率P= 5/9.
（III）
解析
解析已在路上飞奔，马上就到！
知识点
18．设函数
（I）求f(x)的值域和最小正周期；
（II）设A、B、C为△ABC的三内角，它们的对边长分别为a、b、c，若cosC＝
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
21．已知椭圆C的离心率
（I）求椭圆C的方程；
（II）设直线x＝my＋1与椭圆C交于P，Q两点，直线A1P与A2Q交于点S，试问：当m变化时，点S是否恒在一条定直线上？若是，请写出这条直线方程，并证明你的结论；若不是，请说明理由．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
22．已知函数
（1）求
（2）若对任意的实数
（3）若关于
正确答案
解：（1）
当
（3）由
令
当
解析
解析已在路上飞奔，马上就到！
知识点
20．在数列{an}中，
（I）求数列{bn}的通项公式；
（II）求数列
正确答案
解：(1)当n＝1时，
解析
解析已在路上飞奔，马上就到！