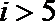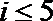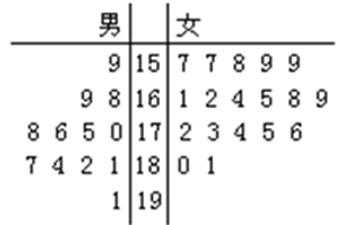- 真题试卷
- 模拟试卷
- 预测试卷
2.设复数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 规定集合




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知各项均为正数的等比数列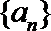

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 如图,圆



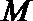
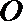

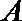

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 图2是某几何体的三视图,其中正视图是腰长为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
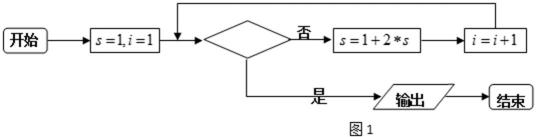
3. 如图1是把二进制数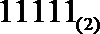
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.在




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
选做题(请考生在第9、10、11三题中任选两题作答,如果全做,则按前两题记分)
9. 如图3,四边形







10.在直









11.若


正确答案
9.
10. 16
11.
解析
解析已在路上飞奔,马上就到!
知识点
12. 把函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 设函数




(i)
(ii)若关于


正确答案
0.15;
解析
解析已在路上飞奔,马上就到!
知识点
13. 已知以双曲线C的两个焦点及虚轴的两个端点为顶点的四边形中,有一个内角为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知


正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
16. 如图4,在杨辉三角中,若某行存在相邻的三个数成等差数列,则称此行为“





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 第4届湘台经贸洽谈交流会于2011年6月在我市举行 ,为了搞好接待工作,大会组委会在某学院招募了12名男志愿者和18名女志愿者。将这30名志愿者的身高编成如下所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”, 身高在175cm以下(不包括175cm)定义为“ 非高个子 ”,且只有“女高个子”才担任“礼仪小姐”。
(1)如果用分层抽样的方法从“高个子”中和“非高个子”中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(2)若从所有“高个子”中选3名志愿者,用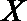
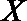
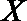
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 在直角坐标系中,已知:




(Ⅰ )求
(Ⅱ )若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图1所示 :在边长为













(I)在底边






(II)求直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.某电视生产企业有A、B两种型号的电视机参加家电下乡活动,若企业投放A、B两种型号电视机的价值分别为a、b万元,则农民购买电视机获得的补贴分别为
(Ⅰ)请你选择自变量,将这次活动中农民得到的总补贴表示为它的函数,并求其定义域;
(Ⅱ)求当投放B型电视机的金额为多少万元时,农民得到的总补贴最大?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 如图,曲线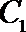
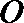
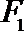
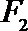
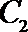
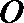
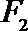
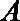
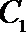
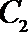
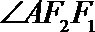
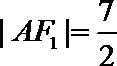
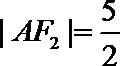
(Ⅰ)求曲线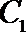
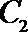
(Ⅱ)过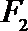

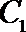
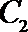
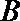
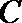
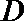
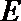
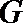
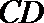

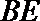
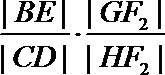
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.设


(Ⅰ)求证:


(Ⅱ)求证: 
正确答案
解析
解析已在路上飞奔,马上就到!