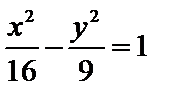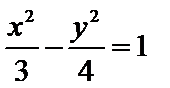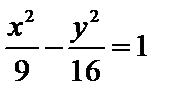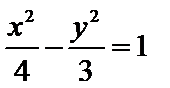- 真题试卷
- 模拟试卷
- 预测试卷
3.已知平面向量








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知等差数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.在△




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知双曲线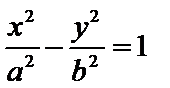
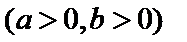
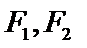
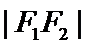

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知定义在R上的函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.某几何体的三视图如图(其中侧视图中的圆弧是半圆),则该几何体的表面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.平面向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知A、B、C是球O的球面上三点,三棱锥O﹣ABC的高为2
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 在椭圆


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.对于定义域为







①
②
③ 
④
其中为“敛1函数”的有__________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知动圆的圆心C在抛物线x2=2py(p>0)上,该圆经过点A(0,p),且与x轴交于两点M、N,则sin∠ MCN的最大值为__________.
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
15.如果直线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数


①当

②函数
③

④
其中正确的命题是___________.
正确答案
③④
解析
解析已在路上飞奔,马上就到!
知识点
13.过点


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.在平面直角坐标系







(Ⅰ)求椭圆C的方程;
(Ⅱ)设P为椭圆上一点,且满足


正确答案
(Ⅰ)∵
则椭圆方程为
设
当

解得

(Ⅱ)设
由

由

∴

由点P在椭圆上,得

又由




则

由①,得
联立②,解得

解析
解析已在路上飞奔,马上就到!
知识点
17.如图所示,扇形AOB,圆心角AOB的大小等于
(1)若C是半径OA的中点,求线段PC的长;
(2)设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 数列








(1)求数列

(2)设




正确答案
(1)∵


当

当

∴
∴数列


∴
设



∴
(2)
∴
∵
∴数列

综上所述,
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2.又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
(1)求证:PC⊥AC;
(2)求二面角M﹣AC﹣B的余弦值;
(3)求点B到平面MAC的距离.
正确答案
方法1:(1)证明:∵PC⊥BC,PC⊥AB,∴PC⊥平面ABC,∴PC⊥AC.
(2)取BC的中点N,连MN.∵PM=∥CN,∴MN=∥PC,∴MN⊥平面ABC.
作NH⊥AC,交AC的延长线于H,连接MH.
由三垂线定理得AC⊥MH,∴∠MHN为二面角M﹣AC﹣B的平面角.
∵直线AM与直线PC所成的角为60°,
∴在Rt△AMN中,∠AMN=60°.
在△ACN中,
在Rt△AMN中,
在Rt△NCH中,
在Rt△MNH中,∵

故二面角M﹣AC﹣B的余弦值为
(3)作NE⊥MH于E.∵AC⊥平面MNH,∴AC⊥NE,∴NE⊥平面MAC,
∴点N到平面MAC的距离为
∵点N是线段BC的中点,
∴点B到平面MAC的距离是点N到平面MAC的距离的两倍为
方法2:(1)证明:∵PC⊥BC,PC⊥AB,∴PC⊥平面ABC,∴PC⊥AC.
(2)在平面ABC内,过C作BC的垂线,并建立空间直角坐标系如图所示.
设P(0,0,z),则

∵
且z>0,∴

设平面MAC的一个法向量为
得


平面ABC的一个法向量为

显然,二面角M﹣AC﹣B为锐二面角,∴二面角M﹣AC﹣B的余弦值为
(3)点B到平面MAC的距离
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数f(x)=alnx+

(I)求实数a的取值范围;
(II)若x1∈(0,


正确答案
(I)由f(x)=alnx+

∵a≠0,令
令

(II)由(I)得:
设ax2﹣(2a+1)x+a=0(0<a<2)的两根为α,β,
则

当x∈(0,α)和(β,+∞)时,
当x∈

则f(x1)≤f A.,f(x2)≥f(β),
则f(x2)﹣f(x1)≥f(β)﹣f(α)=alnβ
=


令

则函数h(x)单调递增, h(x)≥h(2)=2ln2+
∴
∵

∴f(x1)﹣f(x2)≥ln2+
解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22、23两题中任选一题作答。注意:只能做所选定题目。如果多做,则按所做的第一个题目计分。
22.如图,已知⊙O的半径为1,MN是⊙O的直径,过M点作⊙O的切线AM,C是AM的中点,AN交⊙O于B点,若四边形BCON是平行四边形.
(Ⅰ)求AM的长;
(Ⅱ)求sin∠ANC.
23.已知函数
(1)若


(2)当



正确答案
22.(Ⅰ)连接

因为四边形
所以

因为

可得





(Ⅱ)作



故
23.
解析
解析已在路上飞奔,马上就到!