- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.设口袋中有黑球、白球共7个,从中任取2个球,已知取到白球个数的数学期望值为
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
10. 定义某种运算




正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
11.在平面直角坐标系





正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
2.若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.等差数列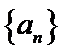
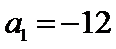
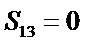
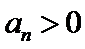
正确答案
8
解析
解析已在路上飞奔,马上就到!
知识点
4.△ABC的内角A、B、C的对边分别为a、b、c,且asinA+csinC-

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设




正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
8.已知圆锥的侧面展开图是一个半径为3cm,圆心角为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.在极坐标系中,若直线






正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
13.对函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.不等式


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.若不等式

正确答案
1或2
解析
解析已在路上飞奔,马上就到!
知识点
14.在实数集







按上述定义的关系“
① 若


② 若

③ 若


④ 对于任意向量



其中真命题的序号为___________
正确答案
① ② ③
解析
解析已在路上飞奔,马上就到!
知识点
15.已知a,b是实数,则“

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设
① 存在

② 存在

③ 三条直线上存在四点

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设P是△ABC所在平面内的一点,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知向量

(1)求函数
(2)当


正确答案
(1)

由

(2)

所以
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,四边形



(1)求证:

(2)求二面角
正确答案
(1)证明:设



因为 四边形

且



因为 


(2)解:因为四边形

所以△
因为




由

设


则

所以 
所以 

设平面

则有

取

易知平面

由二面角

所以二面角
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)若

(2)若函数




正确答案
(1)
解得 
当

(2)由题意,




只有在

所以

解析
解析已在路上飞奔,马上就到!
知识点
22.在平面直角坐标系



(1)求到点


(2)过点







(3)已知点









正确答案
(1)由椭圆方程为







化简得点G的轨迹方程为
(2)由题意可知
故将

可得

(3) 假设存在实数
由已知得


由①②解得

由①③解得

∴

故可得
解析
解析已在路上飞奔,马上就到!
知识点
23.已知数列{an}满足:
(1)求数列{an}的通项公式;
(2)当λ=4时,是否存在互不相同的正整数r,s,t,使得ar,as,at成等比数列?若存在,给出r,s,t满足的条件;若不存在,说明理由;
(3)设Sn为数列{an}的前n项和.若对任意n∈N*,都有(1-λ)Sn+λan≥2λn恒成立,求实数λ的取值范围.
正确答案
(1)当n=1时,a1=3.
当n≥2时,因为
所以
①-②得
所以an=(2n+1)·λn-1(n≥2,n∈N*).
a1=3也适合上式,
所以an=(2n+1)·λn-1 (n∈N*).
(2)当λ=4时,an=(2n+1)·4n-1.
若存在ar,as,at成等比数列,
则[(2r+1) ·4r-1] [(2t+1) ·4t-1]=(2s+1)2 ·42s-2.
整理得(2r+1) (2t+1) 4 r+t -2s=(2s+1)2.
由奇偶性知r+t -2s=0
所以(2r+1) (2t+1)=(r+t+1)2,
即(r-t)2=0.这与r≠t矛盾,
故不存在这样的正整数r,s,t,使得ar,as,at成等比数列.
(3)Sn=3+5λ+7λ2+…+(2n+1)λn-1.
当λ=1时,Sn=3+5+7+…+(2n+1)=n2+2n.
当λ≠1时,Sn=3+5λ+7λ2+…+(2n+1)λn-1,
λSn= 3λ+5λ2+…+(2n-1)λn-1+(2n+1)λn.
(1-λ)Sn=3+2(λ+λ2+λ3++…+λn-1)-(2n+1)λn=3+2×
当λ≠1时,Sn=3+5λ+7λ2+…+(2n+1)λn-1,
要对任意n∈N*,都有(1-λ)Sn+λan≥2λn恒成立,
①当λ=1时,左=(1-λ)Sn+λan=an=2n+1≥2,结论显然成立;
②当λ≠1时,左=(1-λ)Sn+λan=3+2×
=3+2×
因此对任意n∈N*,都有
当0<λ<1时,只要
只要有

因此当0<λ<1时,结论成立.
当λ≥2时,
当1<λ<2时,只要
只要有

因此当1<λ≤
综上所述,实数λ的取值范围为(0,
解析
解析已在路上飞奔,马上就到!









































