- 真题试卷
- 模拟试卷
- 预测试卷
4.设向量a,b满足|a+b|=


正确答案
解析
略
知识点
5.执行下图的程序框图,若输入的

正确答案
解析
略
知识点
2.等比数列{an}的前n项和为Sn.已知S3=a2+10a1,a5=9,则a1=( ).
正确答案
解析
略
知识点
10.在平面上,









正确答案
解析
略
知识点
1.若复数z满足 (3-4i)z=|4+3i |,则z的虚部为 ( )
正确答案
解析
略
知识点
6.4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率( )。
正确答案
解析
略
知识点
7.某几何函数的三视图如图所示,则该几何的体积为( )
正确答案
解析
略
知识点
9.已知点A(-1,0),B(1,0),C(0,1),直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,则b的取值范围是( ).
正确答案
解析
略
知识点
8.已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为( ).
正确答案
解析
略
知识点
3.某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是( )
正确答案
解析
略
知识点
11.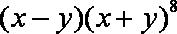
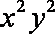
正确答案
-20
解析
略
知识点
12.函数
正确答案
1
解析
略
知识点
14.已知直线






正确答案
解析
略
知识点
15.若关于实数x的不等式|x-5|+|x+3|<a无解,则实数a的取值范围是________.
正确答案
(-∞,8]
解析
略
知识点
13.若函数f(x)=(1-x2)(x2+ax+b)的图像关于直线x=-2对称,则f(x)的最大值是_____。
正确答案
16
解析
略
知识点
19.已知函数

(1)讨论
(2)设



(3)已知
正确答案
见解析。
解析
(1)

(2)g(x)=f(2x)-4bf(x)=











(1) 当b



(2) 当b>2时,若x满足,2< 

g(0)=0,因此当0<X

综上,b的最大值为2
(3) 由(2)知,g(ln


当b=2时,g(ln



当b=

g(ln



ln2<
知识点
20.平面直角坐标系xOy中,过椭圆M:


(1)求M的方程;
(2)C,D为M上两点,若四边形ACBD的对角线CD⊥AB,求四边形ACBD面积的最大值.
正确答案
见解析。
解析
(1)设A(x1,y1),B(x2,y2),P(x0,y0),
则


由此可得
因为x1+x2=2x0,y1+y2=2y0,
所以a2=2b2.
又由题意知,M的右焦点为(
因此a2=6,b2=3.
所以M的方程为
(2)由
解得
因此|AB|=
由题意可设直线CD的方程为
y=
设C(x3,y3),D(x4,y4).
由
于是x3,4=
因为直线CD的斜率为1,
所以|CD|=
由已知,四边形ACBD的面积
当n=0时,S取得最大值,最大值为
所以四边形ACBD面积的最大值为
知识点
16.已知函数


(1)求

(2)若

正确答案
见解析。
解析
(1)
(2)
知识点
18.如图,三棱柱ABC-A1B1C1中,CA=CB,AB=A A1,∠BAA1=60°.
(1)证明AB⊥A1C;
(2)若平面ABC⊥平面AA1B1B,AB=CB=2,求直线A1C 与平面BB1C1C所成角的正弦值。
正确答案
见解析。
解析
(1)取AB中点E,连结CE,

∵AB=



∴


∴AB⊥
(2)由(1)知EC⊥AB,
又∵面ABC⊥面



∴EA,EC,




有题设知A(1,0,0),










设


则



∴

∴直线A1C 与平面BB1C1C所成角的正弦值为
知识点
17.某商场举行的“三色球”购物摸奖活动规定:在一次摸奖中,摸奖者先从装有3个红球与4个白球的袋中任意摸出3个球,再从装有1个蓝球与2个白球的袋中任意摸出1个球.根据摸出4个球中红球与蓝球的个数,设一、二、三等奖如下:
其余情况无奖且每次摸奖最多只能获得一个奖级.
(1)求一次摸奖恰好摸到1个红球的概率;
(2)求摸奖者在一次摸奖中获奖金额X的分布列与期望E(X).
正确答案
见解析。
解析
设Ai表示摸到i个红球,Bj表示摸到j个蓝球,
则Ai(i=0,1,2,3)与Bj(j=0,1)独立.
(1)恰好摸到1个红球的概率为
P(A1)=
(2)X的所有可能值为0,10,50,200,且
P(X=200)=P(A3B1)=P(A3)P(B1)=
P(X=50)=P(A3B0)=P(A3)P(B0)=
P(X=10)=P(A2B1)=P(A2)P(B1)=
P(X=0)=
综上知X的分布列为
从而有E(X)=0×



知识点
21.已知数列{






(1)证明:
(2)是否存在

正确答案
见解析。
解析
(1)由题设



(2)由题设


假设{



证明


数列奇数项构成的数列
令

数列偶数项构成的数列
令

∴

因此,存在存在

















































