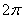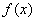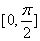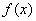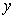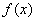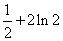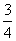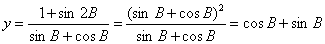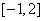- 真题试卷
- 模拟试卷
- 预测试卷
3.曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若偶函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.对任意复数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.给出下列三个命题:
① 若奇函数



② 若函数




③ 函数

其中真命题的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.等比数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知函数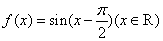
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若二次函数



正确答案

解析
解析已在路上飞奔,马上就到!
知识点
12.函数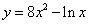
正确答案
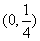
解析
解析已在路上飞奔,马上就到!
知识点
14.已知:数列




① 
② 若前100项中恰好含有30项为0,则
正确答案
9;6或7
解析
解析已在路上飞奔,马上就到!
知识点
13.
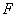
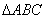
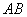
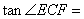
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知:函数
(1)求:
(2)若



正确答案
(1)函数的定义域为
(2)令
解析
解析已在路上飞奔,马上就到!
知识点
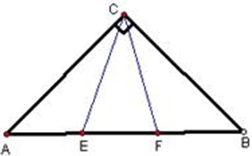
18.已知:△ABC中,角A、B、C所对的三边a,b,c成等比数列。
(1)求证: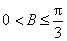
(2)求函数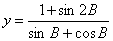
正确答案
解:(1)∵a、b、c成等比数列,
∴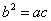
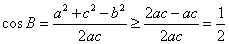
∵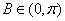
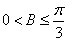
(2)由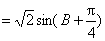
∵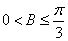
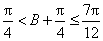
∴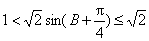
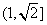
解析
解析已在路上飞奔,马上就到!
知识点
15.已知:函数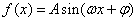
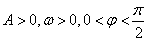

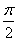
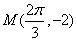
(1)求:
(2)当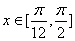
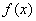
正确答案
(1)由最低点为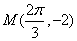

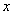
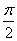
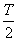
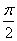
即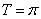
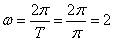
由点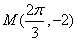
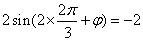
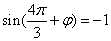
∵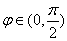
∴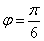
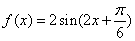
(2)∵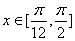
∴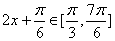
当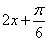
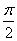
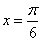

当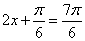
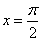
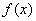
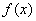
解析
解析已在路上飞奔,马上就到!
知识点
17.已知:对于数列




(1)若数列



(2)若数列

① 设

② 求:

正确答案
解:(1)依题意
(2)①由
∵


故


∴
∵
∴
∴

⑴-⑵得 
∴
解析
解析已在路上飞奔,马上就到!
知识点
19.已知:函数



(1)求:
(2)判断
(3)如果




正确答案
(1)解:令

(2)证明:令

令




(3)∵

∴

∵
∴(1)等价于不等式组:

则

∴
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知:二次函数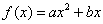
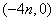
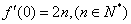
(1)求: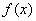
(2)若数列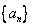
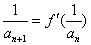
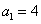
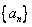
(3)对于(2)中的数列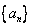
①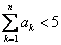
②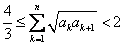
正确答案
解:(1)由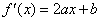
∴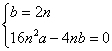
解得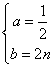
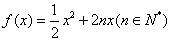
(2)∵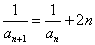
∴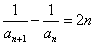
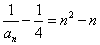
∴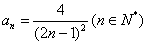
(3)①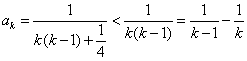
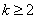
当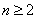
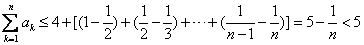
②∵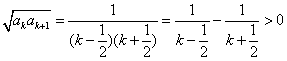
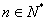
∴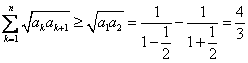
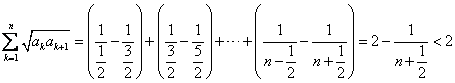
即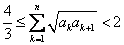
解析
解析已在路上飞奔,马上就到!