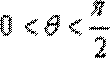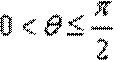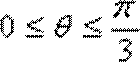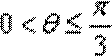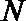- 真题试卷
- 模拟试卷
- 预测试卷
3.某程序框图如图1所示,若该程序运行后输出的值是
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.在正方体ABCD-A1B1C1D1中,点P在线段AD1上运动,则异面直线CP与BA1所成的角的取值范围是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.对于三次函数










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.下列结论正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.等差数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.如图所示,在







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若集合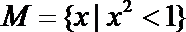
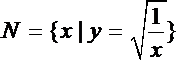
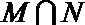
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设复数


正确答案
-2/5
解析
解析已在路上飞奔,马上就到!
知识点
15.若数列








①若

②若


③




④


其中所有真命题的序号是( )
正确答案
①②③
解析
解析已在路上飞奔,马上就到!
知识点
12.直线
正确答案
相交或相切
解析
解析已在路上飞奔,马上就到!
知识点
13.无重复数字的五位数a1a2a3a4a5 , 当a1<a2, a2>a3, a3<a4, a4>a5时称为波形数,则由1,2,3,4,5任意组成的一个没有重复数字的五位数是波形数的概率为( )
正确答案
2/15
解析
解析已在路上飞奔,马上就到!
知识点
14.动点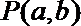
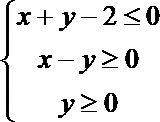
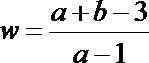
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(1)当


(2)设锐角





正确答案
(1)

所以当

当

(2)因为向量

所以
由余弦定理


解析
解析已在路上飞奔,马上就到!
知识点
18.某公司计划在迎春节联欢会中设一项抽奖活动:在一个不透明的口袋中装入外形一样号码分别为1,2,3,…,10的十个小球。活动者一次从中摸出三个小球,三球号码有且仅有两个连号的为三等奖,奖金30元;三球号码都连号为二等奖,奖金60元;三球号码分别为1,5,10为一等奖,奖金240元;其余情况无奖金。
(1)求员工甲抽奖一次所得奖金ξ的分布列与期望;
(2)员工乙幸运地先后获得四次抽奖机会,他得奖次数
正确答案
(1)甲抽奖一次,基本事件总数为
一等奖的情况只有一种,所以奖金为240元的概率为P(ξ=240)=
三球连号的情况有1,2,3;2,3,4;……8,9,10共8种,所以P(ξ=60)=
仅有两球连号中,对应1,2与9,10的各有7种;对应2,3;3,4;……8,9各有6种。
得奖金30的概率为P(ξ=30)=
奖金为0的概率为P(ξ=0)=
ξ的分布列为:
(2) 由(1)可得乙一次抽奖中中奖的概率为P=
四次抽奖是相互独立的, 所以中奖次数η~B(4,

解析
解析已在路上飞奔,马上就到!
知识点
21.设函数

(1)证明:
(2)当


(3)证明:

正确答案
(1)证明:设
当





即函数



因为



所以
(2)解:当

①当

②假设当



令

因为对任意的正实数

由归纳假设知,
即


因为



即对任意

这就是说,当


由①、②知,当

(3)证明1:先证对任意正整数

由(2)知,当







要证明上式,只需证明对任意正整数

即要证明对任意正整数

以下分别用数学归纳法和基本不等式法证明不等式
①当

②假设当


则
因为
所以
这说明当

综上可知,对任意正整数

解析
解析已在路上飞奔,马上就到!
知识点
17.在数列

(1)求数列

(2)若存在


正确答案
(1)
(2)

设
则



解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在四棱锥







(1)求证:平面

(2)若直线



正确答案
法一(1)取



∴四边形

∵直角△

∴直角△

∴
∵平面


∴
∴
∵
∴

∴平面

(2)设






由△


∵
∴
∵∴
作




∴
∴

∵△

∴
∴
∴
∴
即二面角

法二:
(1)∵平面

平面

∴
又∵
2分
由已知




∴

∴

∴

∴

∴平面
(2)由(Ⅰ),平面

设直线


∴
∵
∴
设平面


由
∴

∴
显然二面角
∴二面角
解析
解析已在路上飞奔,马上就到!
知识点
20.设椭圆E中心在原点,焦点在x轴上,短轴长为4,点Q(2,
(1)求椭圆E的方程;
(2)设动直线L交椭圆E于A、B两点,且
(3)过M(







正确答案
解:(1)因为椭圆E: 

故可求得b=2,a=2
(2)设P(x,y),A(x1,y1),B(x2,y2),当直线L斜率存在时设方程为
解方程组


则△=
即

要使


所以

将它代入()式可得
P到L的距离为
又
将
① 当
由
② 当
③ 当AB的斜率不存在时, 
(3)点P(





故点M(


故直线MN的方程,
设G,H分别是直线MN与椭圆准线,
由


由


故
又P(
有


解析
解析已在路上飞奔,马上就到!