理科数学南开区2016年高三第一次联合考试

立即下载

理科数学热门试卷

X 查看更多试卷

单选题本大题共8小题，每小题5分，共40分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

6. 在中，内角的对边分别为，若的面积为，且，则等于（）

分值: 5分查看题目解析 >

4. 下列说法正确的是（）

A命题“若x2＝1，则x＝1”的否命题为“若x2＝1，则x≠1”

B若，则“”是“”的充分不必要条件

C命题“∃x0∈R，x＋x0＋1<0”的否定是“∀x∈R，x2＋x＋1>0”

D若“”为假，则，全是假命题

分值: 5分查看题目解析 >

5. 已知双曲线C：的离心率，点是抛物线上的一动点，P到双曲线C的上焦点的距离与到直线的距离之和的最小值为，则该双曲线的方程为（） [来源:学*科*

分值: 5分查看题目解析 >

7. 如图，切于点，交于两点，且与直径交于点，，则＝（）

C10

D14

分值: 5分查看题目解析 >

8.已知为偶函数，当时，，若函数恰有4个零点，则实数的取值范围（）

分值: 5分查看题目解析 >

2. 设变量满足约束条件，则目标函数的最大值为（）

D12

分值: 5分查看题目解析 >

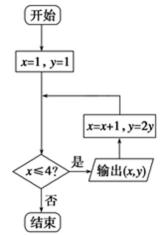
3. 如图所示的程序框图输出的所有点都在函数（）

Ay＝x＋1的图象上

By＝2x的图象上

Cy＝2x的图象上

Dy＝2x-1的图象上

分值: 5分查看题目解析 >

1. 已知全集，集合，则为（）

分值: 5分查看题目解析 >

填空题本大题共6小题，每小题5分，共30分。把答案填写在题中横线上。

9. 是虚数单位，复数_________．

分值: 5分查看题目解析 >

10. 在的二项展开式中，的系数为_________．

分值: 5分查看题目解析 >

14. 如图，在直角梯形中，//是线段上一动点，是线段上一动点，若集合，.则__________．

分值: 5分查看题目解析 >

11. 已知曲线与直线轴围成的封闭区域为A，直线围成的封闭区域为B，在区域B内任取一点，该点落在区域A的概率为_________．

分值: 5分查看题目解析 >

12. 一个机器零件的三视图如图所示，其中俯视图是一个半圆内切于边长为3的正方形，则该机器零件的体积为_________．

分值: 5分查看题目解析 >

13．直线：（为参数），圆：（极轴与x轴的非负半轴重合，且单位长度相同），若圆上至少有三个点到直线的距离恰为，则实数的取值范围为_________．

分值: 5分查看题目解析 >

简答题（综合题）本大题共80分。简答应写出文字说明、证明过程或演算步骤。

17．如图，在四棱锥中，为等边三角形，平面平面，,，，，为的中点．

(Ⅰ) 求证：；

(Ⅱ) 求二面角的余弦值；

(Ⅲ) 若直线与平面所成的角的正弦值为,求实数的值．

分值: 13分查看题目解析 >

20．已知函数，．

(Ⅰ)若函数在上单调递增，求实数的取值范围；

(Ⅱ)若直线是函数图象的切线，求的最小值；

(Ⅲ)当时，若与的图象有两个交点，试比较与的大小．（取为，取为，取为）

分值: 14分查看题目解析 >

15．已知函数，

(Ⅰ)求最小正周期；

(Ⅱ)求在区间上的最大值和最小值.

分值: 13分查看题目解析 >

16．某大学自主招生考试面试环节中，共设置两类考题，A类题有4个不同的小题，B类题有6个不同的小题, 某考生从中任抽取四道题解答.

(Ⅰ)求该考生至少抽取到2道B类题的概率；

(Ⅱ)设所抽取的四道题中B类题的个数为X,求随机变量X的分布列与期望.

分值: 13分查看题目解析 >

18．设椭圆的方程为，点为坐标原点，点的坐标为，点的坐标为，点在线段上，满足，直线的斜率为.

(Ⅰ)求椭圆的离心率；

(Ⅱ)是圆:的一条直径，若椭圆经过，两点，求椭圆的方程．

分值: 13分查看题目解析 >

19．已知非单调数列是公比为的等比数列，且，，记

(Ⅰ)求的通项公式；

(Ⅱ)若对任意正整数，都成立，求实数的取值范围；

(Ⅲ)设数列，的前项和分别为，证明：对任意的正整数，都有

．

分值: 14分查看题目解析 >

真题试卷
模拟试卷
预测试卷

查看更多真题试卷 >

查看更多模拟试卷 >

查看更多预测试卷 >

理科数学 热门试卷

理科数学热门试卷