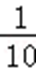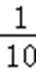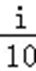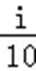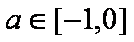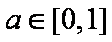- 真题试卷
- 模拟试卷
- 预测试卷
4.设等比数列{an}的前n项和为Sn,若

正确答案
解析
设公比为q,则






知识点
6.已知函数f(x)=
正确答案
解析
由于f(x)=
且f(x)在区间(﹣∞,+∞)上是增函数,
则当x≥0时,y=x2显然递增;
当x<0时,y=x3+a2﹣3a+2的导数为y′=3x2≥0,则递增;
由f(x)在R上单调递增,
则02≥03+a2﹣3a+2,即为a2﹣3a+2≤0,
解得,1≤a≤2.
故选C.
知识点
9.已知点







正确答案
解析
与平面



知识点
3.设x、y是两个实数,命题“x、y中至少有一个数大于1”成立的充分不必要条件是( )
正确答案
解析
若


知识点
7.已知点





正确答案
解析
由点斜式求得线段AB的垂直平分线方程
知识点
8.以下有五个结论:
①某校高三一班和高三二班的人数分别是


②若x1,x2,…,x10的平均数为a,方差为b,则x1+5,x2+5,…,x10+5的平均数为a+5,方差为b+25.;
③从总体中抽取的样本



其中正确结论的个数有( )
正确答案
解析
略。
知识点
2.已知集合A={x|x2≥1},B={x|y=
正确答案
解析
由A中不等式解得:x≥1或x≤﹣1,即A=(﹣∞,﹣1]∪[1,+∞),由B中y=
故选:B。
知识点
5.定义在R上的函数f(x)满足f(x+6)=f(x),当﹣3≤x<﹣1时,f(x)=﹣(x+2)2,当﹣1≤x<3时,f(x)=x.则f(1)+f(2)+f(3)+…+f(2012)=( )
正确答案
解析
∵f(x+6)=f(x),
∴f(x)是以6为周期的函数,
又当﹣1≤x<3时,f(x)=x,
∴f(1)+f(2)=1+2=3,f(﹣1)=﹣1=f(5),f(0)=0=f(6);
当﹣3≤x<﹣1时,f(x)=﹣(x+2)2,
∴f(3)=f(﹣3)=﹣(﹣3+2)2=﹣1,
f(4)=f(﹣2)=﹣(﹣2+2)2=0,
∴f(1)+f(2)+f(3)+f(4)+f(5)+f(6)=1+2﹣1+0+(﹣1)+0=1,
∴f(1)+f(2)+f(3)+…+f(2012)
=[f(1)+f(2)+f(3)+…+f(2010)]+f(2011)+f(2012)
=335×1+f(1)+f(2)
=338.
故选:B.
知识点
10.已知数列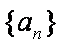
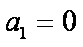
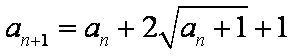
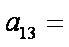
正确答案
解析
由an+1=an+2
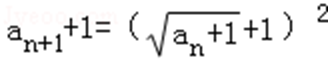
∴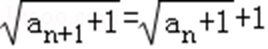
∴{
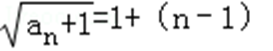
∴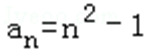
知识点
1.已知i是虚数单位,若z(1+3i)=i,则z的虚部为( )
正确答案
解析
由z(1+3i)=i,得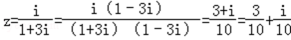
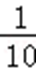
知识点
11.用1,2,3,4,5,6组成数字不重复的六位数,满足1不在左右两端,2,4,6三个偶数中有且只有两个偶数相邻,则这样的六位数的个数为( )
正确答案
解析
从2,4,6三个偶数中任意选出2个看作一个“整体”,方法有

①若1排在左端,方法有





②若1排在右端,同理求得满足条件的六位数也有72种,
③若1排在中间,方法有
根据分步计数原理求得此时满足条件的六位数共有6×

综上,满足条件的六位数共有 72+72+144=288种,
故选B.
知识点
12.函数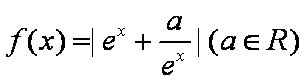
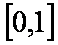
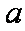
正确答案
解析
当a>0时,y=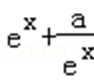
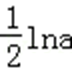
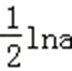
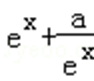
若函数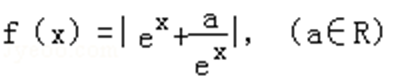
则y=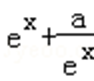
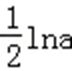
当a=0时,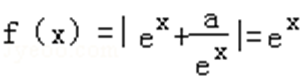
当a<0时,


则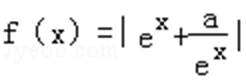


则ln
综上,实数a的取值范围是[﹣1,1],故选C。
知识点
13.能够把圆






上述函数不是圆
正确答案
③
解析
若为和谐函数,则该函数为过原点的奇函数,显然①②④都满足条件,而③不是奇函数,所以不是圆O的和谐函数,所以答案为③。
知识点
14.已知球的直径PQ=4,A、B、C是该球球面上的三点,∠APQ=∠BPQ=∠CPQ=30°,ABC是正三角形,则棱锥P-ABC的体积为_________________.
正确答案
解析
设球心为M,三角形ABC截面小圆的圆心为0,∵ABC是等边三角形,∠APQ=∠BPQ=∠CPQ=30°,∴P在面ABC的投影O是等边△ABC的重心(此时四心合一)∵PQ是直径,∴∠PCQ=90°.∴PC=4cos30°=2

OC=2


OH=

则三棱锥P-ABC体积=




知识点
16.已知函数










正确答案
2
解析
由已知得M(0,2a),N(a,0),因为





知识点
17.已知数列






(1)求证:数列
(2)求

正确答案
见解析。
解析
(1)证明:当





∴由①式可得:当
∴


(2)

当

当

知识点
15.已知直线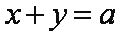
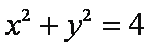
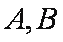

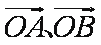
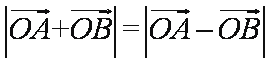
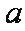
正确答案
±2
解析
因为向量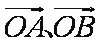
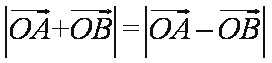
知识点
19.如图所示,圆O的直径为BD,过圆上一点A作圆O的切线AE,过点D作DE⊥AE于点E,延长ED与圆O交于点C.
(1)证明:DA平分∠BDE;
(2)若AB=4,AE=2,求CD的长.
正确答案
见解析。
解析
(1)证明:∵AE是⊙O的切线,∴∠DAE=∠ABD,
∵BD是⊙O的直径,∴∠BAD=90°,
∴∠ABD+∠ADB=90°,
又∠ADE+∠DAE=90°,
∴∠ADB=∠ADE.
∴DA平分∠BDE.
(2)由(1)可得:△ADE∽△BDA,∴
∴
∴∠ABD=30°.
∴∠DAE=30°.
∴DE=AEtan30°=
由切割线定理可得:AE2=DE•CE,
∴
解得CD=
知识点
18.为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据,制表如下:
每名快递员完成一件货物投递可获得的劳务费情况如下:
甲公司规定每件4.5元;乙公司规定每天35件以内(含35件)的部分每件4元,超出35件的部分每件7元.
(1)根据表中数据写出甲公司员工A在这10天投递的快递件数的平均数和众数;
(2)为了解乙公司员工B的每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为

(3)根据表中数据估算两公司的每位员工在该月所得的劳务费.
正确答案
(1)平均数为36,众数为33
(2)E(X)=165.5元
(3)甲公司被抽取员工该月收入4860元,乙公司被抽取员工该月收入4965元.
解析
(1)甲公司员工A投递快递件数的平均数为36,众数为33.
(2)设
当





(3)根据图中数据,可估算甲公司被抽取员工该月收入4860元,乙公司被抽取员工该月收入4965元.
知识点
20.如图,在三棱柱





(1)求证:平面

(2)求直线

(3)求二面角
正确答案
见解析。
解析
(1)取



因为

又

所以

因为


由已知,

所以

所以

又



(2)由(1)知,

坐标原点,


单位长度1,建立如图所示的
空间直角坐标系
由题设知




则


设平面

m




设直线


故
(3)由题设知
可取平面

平面

故

所以二面角

知识点
21.已知中心在原点,焦点在


(1)求椭圆C的方程;
(2)是否存在过点




正确答案
(1)
(2) 存在,
解析
(1)设椭圆C的方程为


(2)假设存在直线l1且由题意得斜率存在,设满足条件的方程为y=k1(x-2)+1,
代入椭圆C的方程得,(3+4k)x2-8k1(2k1-1)x+16k-16k1-8=0.因为直线l1与椭圆C相交于不同的两点A,B,
设A,B两点的坐标分别为(x1,y1),(x2,y2),
所以Δ=[-8k1(2k1-1)]2-4(3+4k)·(16k-16k1-8)=32(6k1+3)>0,所以k1>-.又

即(x1-2)(x2-2)+(y1-1)(y2-1)=,所以(x1-2)(x2-2)(1+

即[x1x2-2(x1+x2)+4](1+

所以




知识点
22.已知函数
(1)当


(2)设函数

(3)若在




正确答案
(1)y=1;
(2)




(3)

解析
(1)

当








(2)
①当





所以








(3)在











所以



因为

②当



所以



③当



因为

此时不存在

综上可得所求