理科数学兰州市2010年高三试卷

精品

单选题
简答题
填空题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、简答题

3、填空题

真题试卷
模拟试卷
预测试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

2．如果复数，则的展开式（按的升幂排列）的第5项是（）

A35

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复数代数形式的乘除运算

题型：单选题

分值: 5分

4．已知，则下列结论中正确的是（）

A函数的周期为

B函数的最小值为

C将的图象向左平移单位后得的图象

D将的图象向右平移单位后得的图象

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的图象与图象变化

题型：单选题

分值: 5分

9. 设实数满足，则有（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

虚数单位i及其性质

题型：单选题

分值: 5分

1．的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

分值: 5分

7．已知函数在上单调递减，那么实数的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

题型：单选题

分值: 5分

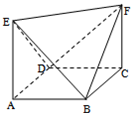
8．如图所示的几何体ABCDEF中，ABCD是平行四边形且AE∥CF，六个顶点任意两点连线能组成异面直线的对数是（）

A36

B28

C39

D20

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线、平面垂直的综合应用

题型：单选题

分值: 5分

3.已知为偶函数，且，当时，，若则

（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

5．设斜率为的直线与椭圆交于不同的两点。且这两点在轴上的射影恰好是椭圆的两个焦点，则该椭圆的离心率为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

6.在样本的频率分布直方图中，共有个小长方形，若其中一个小长方形的面积等于其他个小长方形面积和的四分之一，样本容量为，则该小长方形这一组的频数为（）

A32

B0.2

C40

D0.25

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

10．在平面直角坐标系中，已知点，如果动点P满足，那么的最大值是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

11.若条件满足则的最小值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

题型：单选题

分值: 5分

12. 已知在区间上是减函数，那么（）

A有最大值

B有最大值

C有最小值

D有最小值

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

简单复合函数的导数

简答题（综合题）本大题共70分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 10分

17．已知为坐标原点，。

（1）求的单调递增区间；

（2）若的定义域为，值域为，求的值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

简单复合函数的导数

题型：简答题

分值: 12分

20.设是正数组成的数列，其前项和为，并且对于所有的正整数，与的等差中项等于与的等比中项。

（1）求数列的通向公式；

（2）令，求。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：简答题

分值: 12分

18.从北京到西安的某三列火车正点到达的概率分别为。求：

（1）这三列火车恰有两列正点到达的概率；

（2）这三列火车正点到达列数的数学期望。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线的倾斜角与斜率

题型：简答题

分值: 12分

19．如图，已知四棱锥P—ABCD的底面是直角梯形，，AB=BC=PB=PC=2CD=2，侧面底面ABCD，O是BC中点，AO交BD于E。

（1）求证：；

（2）求二面角的大小；

（3）求证：平面平面PAB。

正确答案

解析

知识点

直线与平面平行的判定与性质

题型：简答题

分值: 12分

21. 如图，已知双曲线C：的右准线与一条渐近线交于点M，F是双曲线C的右焦点，O为坐标原点。

（I）求证：；

（II）若且双曲线C的离心率，求双曲线C的方程；

（III）在（II）的条件下，直线过点A（0，1）与双曲线C右支交于不同的两点P、Q且P在A、Q之间，满足，试判断的范围，并用代数方法给出证明。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：简答题

分值: 12分

22. 已知函数为实常数。

（1）若在上是单调函数，求的取值范围；

（2）当时，求的最小值；

（3）设各项均为正数的无穷数列满足,证明：。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

填空题本大题共4小题，每小题5分，共20分。把答案填写在题中横线上。

题型：填空题

分值: 5分

13．不等式（x－1）|x2－2x－3|≥0的解集为_________．

正确答案

或

解析

解析已在路上飞奔，马上就到！

知识点

一元二次不等式的解法

题型：填空题

分值: 5分

15．已知的三个顶点在同一球面上，若球心到平面的距离为1，则该球的半径______。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

诱导公式的作用

题型：填空题

分值: 5分

14．霓红灯的一个部位由七个小灯泡组成，如图：○○○○○○○，每个灯泡均可亮出红色或黄色，现设计每次变换只闪亮其中三个灯泡，且相邻两个不同时亮，则一共可呈现____________种不同的变换形式。（用数字作答）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

随机事件的关系

题型：填空题

分值: 5分

16．已知且关于的函数在上有极值，则的夹角范围为_____。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

向量的加法及其几何意义

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷