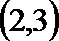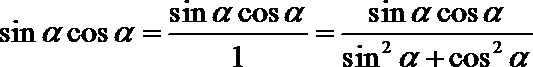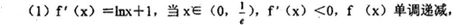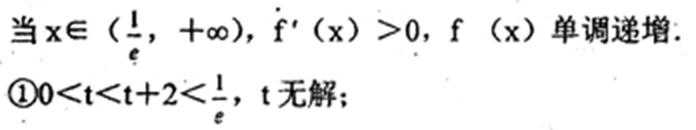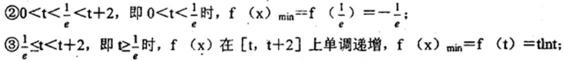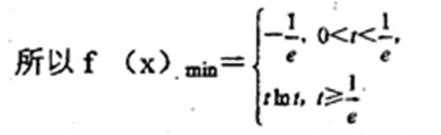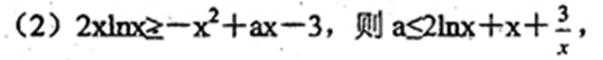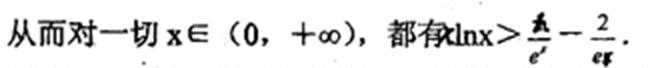理科数学烟台市2013年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

1．集合＞则下列结论正确的是（）

正确答案

解析

，所以，所以，选D．

知识点

二次函数的应用

题型：单选题

分值: 5分

2．若则（）

Aa＜b＜c

Ba＜c＜b

Cc＜a＜b

Db＜c＜a

正确答案

解析

，因为，所以，选B．

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

5．曲线在点处的切线与坐标轴所围三角形的面积为（）

正确答案

解析

，所以在点的导数为，即切线斜率为，所以切线方程为，令得，，令，得．所以三角形的面积为，选A．

知识点

函数单调性的性质

题型：单选题

分值: 5分

4．和是方程的两根，则p、q之间的关系是（）

正确答案

解析

根据根与系数之间的关系可得，所以，即，所以，选D．

知识点

两角和与差的正切函数

题型：单选题

分值: 5分

6．已知、都是锐角，则=（）

正确答案

解析

因为是锐角，所以，又，所以，所以，．

又，选C．

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

10．函数的图象大致是（）

正确答案

解析

函数为奇函数，所以排除A．当时，，排除D．函数为奇函数，且，令得，由于函数为周期函数，而当时，，当时，，则答案应选C．

知识点

函数的值域

题型：单选题

分值: 5分

3．下列函数中，既是偶函数，又是在区间上单调递减的函数是（）

正确答案

解析

非奇非偶函数，排除B,当时，函数单调递增，排除C, 在定义域上不单调，排除D,选A．

知识点

函数单调性的判断与证明函数奇偶性的判断

题型：单选题

分值: 5分

7．函数在上为减函数，则的取值范围是（）

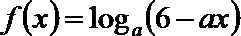
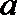
正确答案

解析

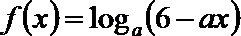
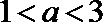
因为函数在上为减函数，则有且，解得，选B．

知识点

复合函数的单调性对数函数的单调性与特殊点

题型：单选题

分值: 5分

8．如果函数的图像关于点中心对称，那么的最小值为（）

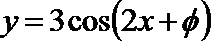
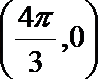
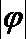
正确答案

解析

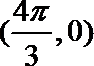
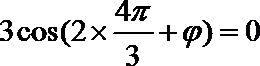
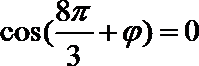
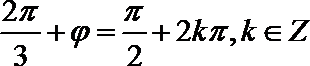
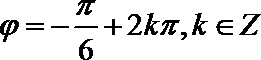
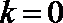
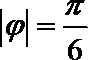
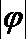
函数关于点对称，则有，即，所以，即，即，所以当时，，此时最小，选A．

知识点

双曲线的几何性质

题型：单选题

分值: 5分

9．由直线，曲线及轴所谓成图形的面积为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

定积分的简单应用

题型：单选题

分值: 5分

12．函数的图象如下，则等于（）

B503

C1006

D2012

正确答案

解析

由图象可知，函数的最大值为，最小值为，解得，函数的周期，即，所以，所以，当时，，所以，所以，即．在一个周期内，所以，选D．

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

11．下图是函数的部分图像，则函数的零点所在的区间是（）

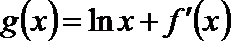
正确答案

解析

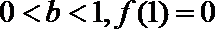
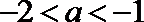
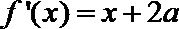
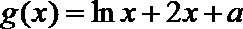
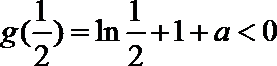
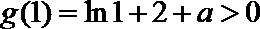
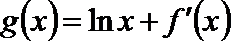
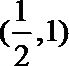
由函数图象可知，从而，，所以，函数在定义域内单调递增，，，所以函数的零点所在的区间是，选C．

知识点

函数零点的判断和求解导数的运算

填空题本大题共4小题，每小题4分，共16分。把答案填写在题中横线上。

题型：填空题

分值: 4分

13．若则（）．

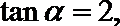
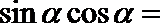
正确答案

解析

．

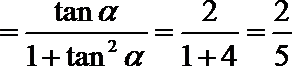
知识点

二次函数的应用

题型：填空题

分值: 4分

14．若方程的两根满足一根大于2，一根小于1，则m的取值范围是（）．

正确答案

解析

令函数，由题意可知，即，所以，即．

知识点

指数函数的图像变换

题型：填空题

分值: 4分

16．关于函数有下列命题：

①函数的周期为；

②直线是的一条对称轴；

③点是的图象的一个对称中心；

④将的图象向左平移个单位，可得到的图象．

其中真命题的序号是（）．（把你认为真命题的序号都写上）

正确答案

①③

解析

，所以周期，所以①正确，当时，不是最值，所以②不正确．，所以③正确．将的图象向左平移个单位，得到，所以④不正确，综上正确的命题为①③．

知识点

命题的真假判断与应用三角函数的周期性及其求法正弦函数的对称性函数y=Asin（ωx+φ）的图象变换三角函数中的恒等变换应用

题型：填空题

分值: 4分

15．设定义在R上的函数同时满足以下条件；

①；

②；

③当时，．

则（）．

正确答案

解析

由得，所以函数为奇函数．由，可知函数的周期为2，所以，，，由②知，所以，所以．

知识点

导数的乘法与除法法则

简答题（综合题）本大题共74分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

20．已知一家公司生产某种品牌服装的年固定成本为10万元，每生产1千件需另投入2．7万元．设该公司一年内生产该品牌服装x千件并全部销售完，每千件的销售收入为万元，且

（1）写出年利润W（万元）关于年产量x（千件）的函数解析式；

（2）年产量为多少千件时，该公司在这一品牌服装的生产中所获得的年利润最大。（注：年利润一年销售收入一年总成本）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的最值及其几何意义分段函数模型函数模型的选择与应用

题型：简答题

分值: 12分

17．已知

（1）若，求实数m的取值范围；

（2）是否存在实数m，使得“”是“”的充要条件，若存在，求出m的取值范围；若不存在，请说明理由。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：简答题

分值: 12分

18．设．

（1）求的最小值及此时的取值集合；

（2）把的图象向右平移m（m＞0）个单位后所得图象关于y轴对称，求m的最小值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：简答题

分值: 12分

21．在三角形ABC中，角A、B、C满足。

（1）求角C的大小；

（2）求函数的值域。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数幂的运算

题型：简答题

分值: 14分

22．已知函数。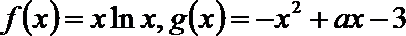

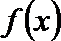
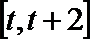
（1）求函数在（t＞0）上的最小值；

（2）对一切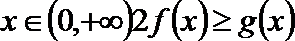恒成立，求实数a的取值范围；

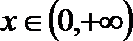
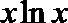
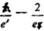
（3）求证：对一切，都有＞。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：简答题

分值: 12分

19．已知函数

（1）求的单调递减区间；

（2）若在区间上的最大值为20，求它在该区间上的最小值。

正确答案

（2）

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷