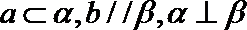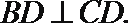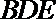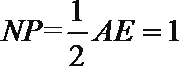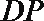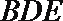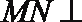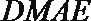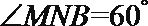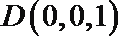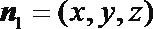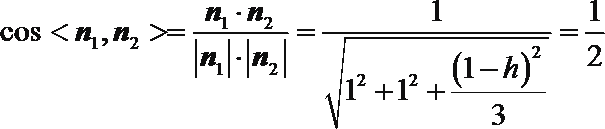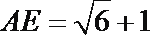- 真题试卷
- 模拟试卷
- 预测试卷
1.设全集



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
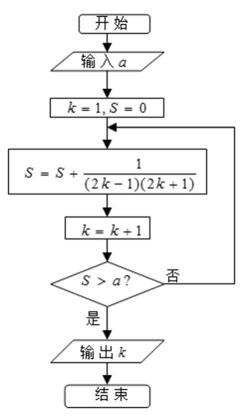
4. 阅读如图所示的程序框图,若输入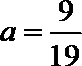
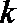
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 现有三个小球全部随机放入三个盒子中,设随机变量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 已知命题

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.一个几何体的三视图如图所示,则该几何体的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设不等式组


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 设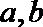
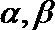
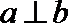
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设




正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
12.在平面直角坐标平面上,





正确答案
2/5
解析
解析已在路上飞奔,马上就到!
知识点
13. 一个棱长为6的正四面体纸盒内放一个正方体,若正方体可以在纸盒内任意转动,则正方体棱长的最大值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.由1,2,3,4,5,6组成没有重复数字的六位数,要求奇数不相邻,且4不在第四位,则这样的六位数共有( )个.
正确答案
120
解析
解析已在路上飞奔,马上就到!
知识点
15.平面向量







正确答案
5/4
解析
解析已在路上飞奔,马上就到!
知识点
16.已知






正确答案

解析
解析已在路上飞奔,马上就到!
知识点
17.已知集合



①
②
③
④
其中是“垂直对点集”的序号是( )
正确答案
②④
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知函数










(1)证明:
(2)若




正确答案
(1)由题意知:

(2)因为





当且仅当


解析
解析已在路上飞奔,马上就到!
知识点
19. 某工厂为扩大生产规模,今年年初新购置了一条高性能的生产线,该生产线在使用过程中的维护费用会逐年增加,第一年的维护费用是4万元,从第二年到第七年,每年的维护费用均比上年增加2万元,从第八年开始,每年的维护费用比上年增加25%
(1)设第


(2)若该生产线前n年每年的平均维护费用大于12万元时,需要更新生产线,求该生产线前

正确答案
(1)
(2)第10年年初
解析
解析已在路上飞奔,马上就到!
知识点
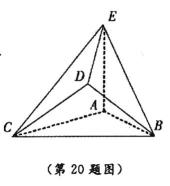
20. 在如图所示的几何体中,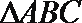
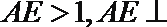
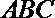
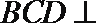
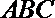
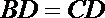
(1)若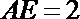
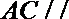
(2)若二面角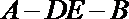
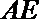
正确答案
(1)分别取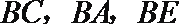
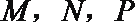
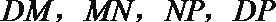
则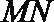
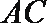
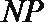
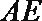
因为
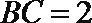
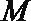
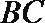
所以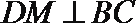
又因为平面
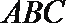
所以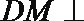
又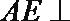
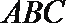
所以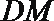
所以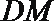
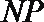
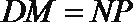
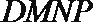
所以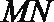

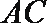
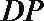

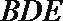
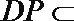
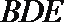
所以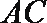
(或者建立空间直角坐标系,求出平面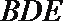
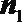


过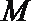
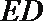
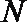
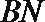
因为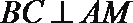
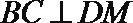
所以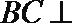
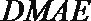
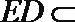
则有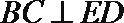
所以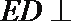
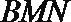
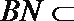
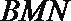
所以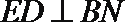
所以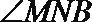
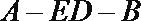
即
在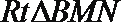
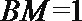
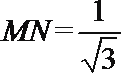
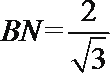
在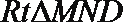
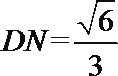
设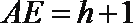
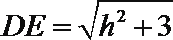
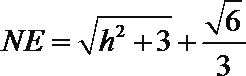
在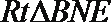
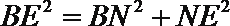
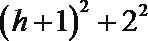
解得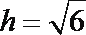
解法二:

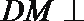
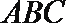
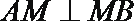
建立如图所示的空间直角坐标系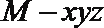
设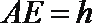
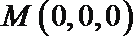
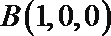
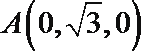
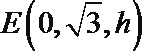
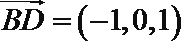
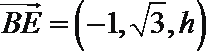
设平面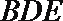
则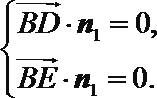
所以
令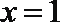
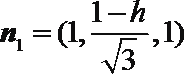
又平面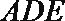
所以
解得
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知椭圆C:



(1)若

(2)是否存在这样的椭圆C,使得
正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
22. 设
(1)若

(2)已知正数



(3)已知



正确答案


















即证
① 当
② 假设当



即当



这说明当
综上①②知,当


解析
解析已在路上飞奔,马上就到!