- 真题试卷
- 模拟试卷
- 预测试卷
3.已知



比数列,则( )
正确答案
解析
试题分析:利用公差不为0的等差数列中

设等差数列{








故选B.
考查方向
解题思路
根据等差数列的通项公式,等比数列的性质,求出首项和公差d的关系,然后利用首项表示出前4项和,判断出符号.
易错点
要熟记的等差数列和等比数列的通项公式和前n项和公式.
知识点
4.命题“
正确答案
解析
试题分析:由全称命题的否定是特称命题,得出结论即可。
“


故选D.
考查方向
解题思路
根据全称命题的否定,把任意改为存在,然后否定结论即可.
易错点
注意含有量词的命题的否定中把任意改为存在,且的否定为或.
知识点
5.如图,设抛物线


正确答案
解析
试题分析:如图作出抛物线的准线,经过A、B分别向准线作垂线,利用三角形相似
和抛物线的性质,求出三角形面积的比值。
作抛物线的准线x=-1,经过A、B分别向准线作垂线,垂足分别为E,D,与y轴分别
交于N,M,由抛物线的定义可知|BF|=|BD|,|AF|=|AE,|BM||=|BD|-1=|BF|-1,
|AN||=|AE|-1=|AF|-1,∴
考查方向
解题思路
作出抛物线的准线,经过A、B分别向准线作垂线,利用三角形的面积公
式,把三角形面积的比值利用三角形相似进行转化.
易错点
注意正确求出抛物线的准线.
知识点
8.如图,已知△ABC,D是AB的 中点,沿直线CD将△ACD折成△A′CD,所成二面角A′-CD-B的平面角为α,则( )
正确答案
解析
试题分析:分AC=BC和AC≠BC两种情况,作出二面角的平面角进行判断。
当AC=BC时,∠A′DB为二面角A′-CD-B的平面角,∠A′DB=α;
当AC≠BC时,∠A′DB>α,故选B.
考查方向
解题思路
作出二面角的平面角,然后进行判断即可。
易错点
注意角的关系中等号成立的条件。
知识点
1.已知集合P={

正确答案
解析
试题分析:由集合P={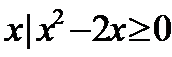

P={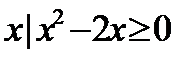


考查方向
解题思路
首先由集合P中的元素满足的不等式求出集合P,然后求出集合P的补集,
最后求出集合P的补集与集合Q的交集.
易错点
求集合P的过程中不要忘了等号.
知识点
6.设A,B是有限集,定义d(A,B)=card(A,B)=card(A∪B)-card(A∩B),其中card(A)表示有限集A中的元素个数,
命题①:对任意有限集A,B,“A≠B”是“d(A,B)>0”的充分必要条件;
命题②:对任意有限集A,B,C,d(A,C)≤d(A,B)+d(B,C),
正确答案
解析
试题分析:根据充分性和必要性判断出命题①正确;根据集合间的关系判断出命
题②正确。
命题①:对任意有限集A,B,若“A≠B”,则A∪B≠A∩B,则card(A∪B)>car(A∩B),
故“d(A,B)>0”成立,
若d(A,B)>0”,则card(A∪B)>card(A∩B),则A∪B≠A∩B,故A≠B成立,故
命题①成立,
命题②,d(A,B)=card(A∪B)-card(A∩B),d(B,C)=card(B∪C)-card
(B∩C),
∴d(A,B)+d(B,C)=card(A∪B)-card(A∩B)+card(B∪C)-card(B∩C)=[card
(A∪B)+card(B∪C)]-[card(A∩B)+card(B∩C)]
≥card(A∪C)-card(A∩C)=d(A,C),故命题②成立,
故选:A:
考查方向
解题思路
根据充分必要条件的条件进行判断命题①;借助新定义和集合的运算判断命
题②,从而得出结论.
易错点
充分必要条件要从充分性和必要性两个方面来证明.
知识点
7.存在函数f(x)满足,对任意x∈R都有( )
正确答案
解析
试题分析:对于A,通过取x=0和
过x取0和π,可得出f(0)有两个不同的值;对于C,通过x取±1,可得出f(2)有两个
不同的值,根据函数的定义可判断出这三项不正确,得出结论。
A.取x=0,则sin2x=0,∴f(0)=0,取
值不符合函数的定义;
B. 取x=0,则f(0)=0,取x=π,则
C.取x=1,则f(2)=2,取x=-1,则f(2)=0;f(2)有两个值不符合函数的定义;
D.令x+1=t,则



∴


故选D.
考查方向
解题思路
通过取特殊值和函数的定义进行判断.
易错点
对函数概念的理解.
知识点
2.某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )
正确答案
解析
试题分析:由几何体的三视图确定几何体的形状,求出几何体的体积。
由三视图可知几何体是下部为棱长为2的正方形,上面是底面边长为2的正方形、高为2的正四棱锥,∴几何体的体积为


考查方向
解题思路
判断几何体的形状,利用三视图的数据,求几何体的体积即可.
易错点
求棱锥的体积是不要忘记乘
知识点
11.函数
正确答案

解析
试题分析:由三角函数中的公式把函数转化为一个角的三角函数,然后利用周期公式和正弦函数的单调性求出函数的单调递减区间。

∴函数的最小正周期为T =π;
由

∴函数的单调递减区间为[
考查方向
解题思路
根据二倍角公式和两角差的正弦公式,把函数转化为一个角的三角函数

易错点
要熟记三角函数中的公式,正确利用公式把函数转化为一个角的三角函数.
10.已知函数
正确答案
0;
解析
试题分析:利用分段函数的解析式求出函数值和函数的最小值。
∵
当x≥1时,

当x<1时,f(x)≥0,当且仅当x=0时取得最小值,所以函数的最小值为
考查方向
解题思路
根据分段函数的解析式,首先求出f(-3)的值为,再求出f(f(-3))的值;分别求
出函数在两段上的最小值,比较得出函数的最小值。
易错点
分段函数求值要代入到对应的解析式中,注意基本不等式等号成立的条件。
知识点
9.双曲线
正确答案


解析
试题分析:由双曲线

∵双曲线




考查方向
解题思路
根据双曲线的方程求出2c和渐近线方程。
易错点
注意双曲线中焦距为2c,双曲线的渐近线方程。
知识点
12.若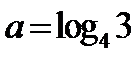
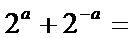
正确答案

解析
试题分析:根据指数式与对数式的关系求出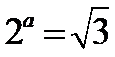
∵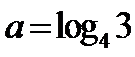

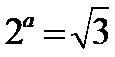
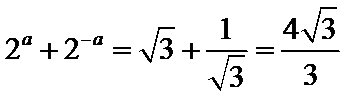
考查方向
解题思路
由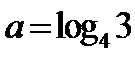
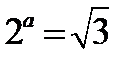
易错点
要正确应用指数的运算法则.
知识点
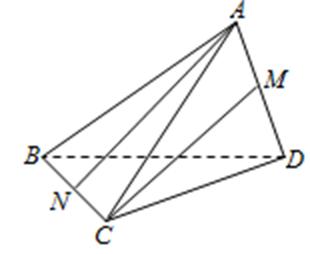
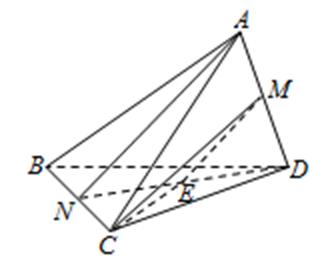
13.如图,三棱锥A-BCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别是AD,BC的中点,则异面直线AN,CM所成的角的余弦值是 .
正确答案
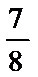
解析
试题分析:利用中位线作出异面直线所成的角,然后在三角形中利用余弦定理求出余弦值即可。
连结ND,取ND 的中点为E,连结ME,则ME∥AN,异面直线AN,CM所成的角就是∠EMC,
∵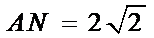
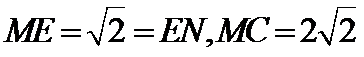
又∵EN⊥NC,∴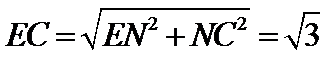
∴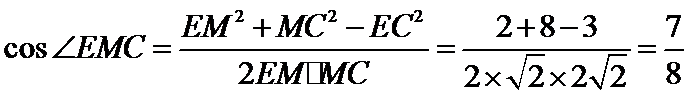
故答案为: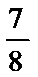
考查方向
解题思路
连结ND,取ND 的中点为E,连结ME说明异面直线AN,CM所成的角
就是∠EMC通过解三角形,求解即可.
易错点
异面直线所成的角为锐角或直角.
知识点
15.已知







正确答案
1;2;
解析
试题分析:利用向量模的平方及取到的最小值进行转化,求出值即可。
∵






∴
考查方向
解题思路
根据空间向量的模的平方等于向量数量积的平方,由向量模的最小值进行转
化,利用取得最小值时的条件求解.
易错点
空间向量模的平方的运算.
知识点
14.若实数x,y满足
正确答案
3;
解析
试题分析:由直线与圆的位置关系,分类讨论去掉绝对值,利用线性规划求出最小值。
由
当2x+y-2>0时,|2x+y-2|+|6-x-3y |=x-2y+4,则可知当
可知当
综上所述,|2x+y-2|+|6-x-3y |的最小值为3.
考查方向
解题思路
根据直线与圆的位置关系,可得出6-x-3y>0,然后根据2x+y-2与0的
大小关系,去掉绝对值,利用线性规划的知识求出最小值.
易错点
注意利用直线与圆的位置关系去掉绝对值符号.
知识点
如图,在三棱柱






17.证明:


18.


正确答案
详见解析;
解析
试题分析:由条件设E为BC的中点,可证得AE⊥平面

考查方向
解题思路
由线面垂直的判定定理,两平行线中的一条垂直于一个平面,另一条也垂
直于这个平面,得出结论;的余弦值.
易错点
注意二面角的取值范围,分清是锐角还是钝角.
正确答案

解析
作




设E为BC的中点,由题意可得
∴


由D,E分别为



∴四边形


∴













由





由余弦定理得,
考查方向
解题思路
作出二面角的平面角,在三角形中利用余弦定理求出二面角
的余弦值.
易错点
注意二面角的取值范围,分清是锐角还是钝角.
19.已知函数

(1)证明:当|a|≥2时,M(a,b)≥2;
(2)当a
正确答案
(1)详见解析;(2)3;
解析
试题分析:(1)分析题意可知





(1)由f(x)= 














(2)由M(a,b)








考查方向
解题思路
(1)根据a的取值范围,得到函数在[-1,1]上的单调性,分类讨论证得结论;(2)由题中给出的新定义进行求解.
易错点
二次函数在闭区间上的单调性.
知识点
16.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知

(1)求tanC的值;
(2)若△ABC的面积为7,求b的值。
正确答案
(1)2;(2)b=3;
解析
试题分析:根据正弦定理可将条件中的边之间的关系转化为角之间的关系,再将式子作三角恒等变型即可求解;(2)根据条件首先求得
(1)由






(2)由



又∵


又∵


考查方向
解题思路
(1)利用正弦定理和三角函数的诱导公式,同角三角函数的关系式进行化简
求解;(2)求出角C的正弦和余弦值,再求出sinB,由正弦定理求出c,最后利用三角形的面
积求出b的值.
易错点
注意三角函数中公式的应用.
知识点
20.已知椭圆


(1)求实数m的
(2)求△AOB面积的最大值(O为坐标原点).
正确答案
(1)


解析
试题分析:(1)可设直线AB的方程为y=



(1)由题意可知m











(2)令



∴S(t)=




考查方向
解题思路
(1)设出直线AB的方程,把椭圆和直线方程联立,利用中点的坐标公式,根
与系数的关系求解;(2)表示出三角形的面积,利用二次函数求出最大值即可.
易错点
计算要细心.
知识点
21.(本题满分15分)
已知数列






(1)证明:1

(2)设数列



正确答案
(1)详见解析;(2)详见解析;
解析
试题分析:(1)首先根据递推公式可得





(1)由题意得,







(2)由题意得






考查方向
解题思路
(1)根据题意,首先求出

易错点
对数列的通项公式要灵活变形.