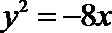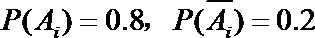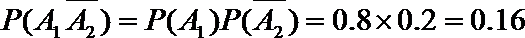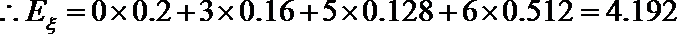- 真题试卷
- 模拟试卷
- 预测试卷
6.下面是一个算法的程序框图,当输入的


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.在边长为1的正方体中,
















正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.原点与极点重合,

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如果直线y=kx+1与圆


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.样本容量为200的频率分布直方图如右图所示,根据样本频率分布直方图估计, 样本数据落在

正确答案
64; 0.4
解析
解析已在路上飞奔,马上就到!
知识点
11.已知









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.代数式

正确答案
9. 0
解析
解析已在路上飞奔,马上就到!
知识点
13.已知斜率为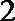
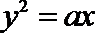
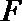
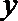
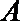
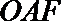
正确答案
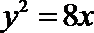
解析
解析已在路上飞奔,马上就到!
知识点
12.如图,CE为圆O的直径,PE为圆O的切线,E为切点,PBA为圆O的割线,交CE于D点,CD=2,AD=3,BD=4,则圆O的半径为
正确答案
4;20
解析
解析已在路上飞奔,马上就到!
知识点
14. 如果对于函数






则 ①
②
③
④
四个函数中为不严格增函数的是( ),
若已知函数







正确答案
①③;10.
解析
解析已在路上飞奔,马上就到!
知识点
16. 如图,在四棱锥







(1)求证:

(2)求证:平面

(3)





正确答案
(1)设



∵

∴在△


∵





(2)









又


在










(3)
如图建立坐标系,设AE=1,则B(2,0,0),D(0,1,2),C(2,0,2),F(1,0,1),
设P(0,a ,0),




由




令

设



由







即P在E处
解析
解析已在路上飞奔,马上就到!
知识点
18.函数
(1)试求
(2)求证:不等式

正确答案
(1)
当

当



(2)由于

因此只需证

作函数

则
在(1)中取

由(1)知
从而有

于是
所以
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知椭圆




(Ⅰ)求椭圆的方程;
(Ⅱ)已知直线




正确答案
(Ⅰ)方法1:由已知得直线

即 
根据点到直线的距离公式得:
即:
又 

由①②③联立得:
∴椭圆的方程为:
方法2:∵

故
即
以下同解法1.
(Ⅱ)设


由

则
=
=
∴
∴
而

故 
∴
即
解得:
∴

解析
解析已在路上飞奔,马上就到!
知识点
20. 设






(1)对于排列4,2,5,1,3,求
(2)对于项数为2n-1 的一个排列,若要求2n-1为该排列的中间项, 试求
(3)证明
正确答案
(1)由题意可知, 



所以 对于排列4,2,5,1,3, 

(2) 此排列为
所以 

(3)证明 考虑集合

一方面,固定



另一方面,固定



所以得
解析
解析已在路上飞奔,马上就到!
知识点
15.设
(Ⅰ)求
(Ⅱ)若锐角


正确答案
(Ⅰ)

故


(Ⅱ)由


又由



从而
解析
解析已在路上飞奔,马上就到!
知识点
17. 某射击游戏规定:每位选手最多射击3次;射击过程中若击中目标,方可进行下一次射击,否则停止射击;同时规定第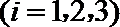


(Ⅰ)求甲恰好射击两次的概率;
(Ⅱ)设该选手甲停止射击时的得分总和为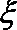
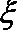
正确答案
(Ⅰ)设选手甲第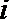
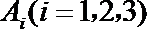
则
依题可知: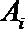
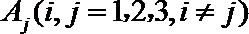
所求为:
(Ⅱ)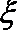
分布列为:
解析
解析已在路上飞奔,马上就到!