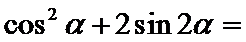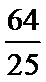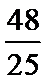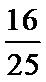- 真题试卷
- 模拟试卷
- 预测试卷
2.若

正确答案
解析

考查方向
解题思路
写出z的共轭,然后应用乘法、除法运算化简。
易错点
在除法运算中,关键是“分母实数化”(分子、分母同乘以分母的共轭复数),此时要注意区分(a+bi)(a-bi)=a2+b2与(a+b)(a-b)=a2-b2,防止实数中的相关公式与复数运算混淆,造成计算失误.
知识点
3.已知向量


正确答案
解析
由题意,得

考查方向
解题思路
利用向量的夹角公式求余弦,然后根据余弦值求角。
易错点
向量数量积以及模的运算。
知识点
8.在


正确答案
解析
设





考查方向
解题思路
利用三角形边角关系以及余弦定理变形求余弦值。
易错点
公式的变形,三角形中基本量的应用与求解。
知识点
1.设集合
正确答案
考查方向
解题思路
化简集合S(即解不等式),然后求S∩T。
易错点
不等式的解法,数轴表示集合。
知识点
4.某旅游城市为向游客介绍本地的气温情况,绘制了一年中月平均最高气温和平均最低气温的雷达图。图中A点表示十月的平均最高气温约为15°C,B点表示四月的平均最低气温约为5°C。下面叙述不正确的是
正确答案
考查方向
解题思路
根据图中的最高气温和最低气温线观察分析。
易错点
审题要清晰,答案要求找不正确的;再者读图要细致,根据选择支语句加强讨论。
知识点
5.若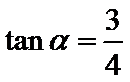
正确答案
解析
由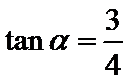
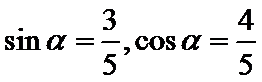
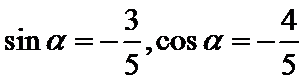
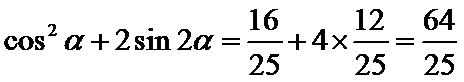
考查方向
解题思路
由正切值求正弦余弦,然后结合倍角公式求值。
易错点
三角函数值的符号问题,三角公式的应用
知识点
6.已知


正确答案
解析
因为


考查方向
解题思路
先将幂值统一成同底数的问题,再结合指数函数的性质以及幂函数的性质比较大小
易错点
幂值的化简,指数函数、幂函数的性质。
知识点
7.执行下图的程序框图,如果输入的
正确答案
考查方向
解题思路
根据循环结构逐一运算,直到满足输出条件终止循环,输出结果.
易错点
循环的终止条件和控制循环变量求解。
知识点
12.定义“规范01数列”{an}如下:{an}共有2m项,其中m项为0,m项为1,且对任意

正确答案
解析
由题意,得必有

考查方向
解题思路
将所有规范01数列列表,根据表格找出适合条件的数列。
易错点
注意列表的规范性,避免重复与遗漏。
知识点
9.如图,网格纸上小正方形的边长为1,粗实现画出的是某多面体的三视图,则该多面体的表面积为
正确答案
解析
该三视图是以侧视图为底面的斜四棱柱
考查方向
解题思路
根据三视图还原几何体,然后结合数据应用表面积公式求解.
易错点
注意还原几何体时把握几何体的结构特征。
知识点
10.在封闭的直三棱柱




正确答案
解析
要使球的体积



考查方向
解题思路
根据球的内切外接特点,结合棱柱的结构特征求出球的体积最值。
易错点
注意球的组合体中半径的求法。
知识点
11.已知O为坐标原点,F是椭圆C:


正确答案
考查方向
解题思路
结合直线方程,三角形相似关系通过成比例的方程关系转化求解。
易错点
构造离心率的等量关系。
知识点
13.若


正确答案
解析
考查方向
解题思路
画出不等式组表示的平面区域,根据目标函数几何意义(本例理解为截距)求解。
易错点
线性规划问题的解题,首先要注意“直线定界,特殊点定域”的原则画好平面区域,再者注意目标函数的几何意义求最值,一般与截距、斜率、距离等问题有关。
知识点
14.函数

单位长度得到.
正确答案
解析
因为





考查方向
解题思路
先根据和角公式化简函数,再根据图像变换分析平移量。
易错点
平移的单位数量问题,要注意是否先进行了周期变换。
知识点
15.已知




正确答案
解析
根据函数求出切线斜率,即可求出切线方程
考查方向
解题思路
先根据偶函数性质求出解析式,然后结合导数求切线方程。
易错点
函数的奇偶性问题,导数求解时出现失误。
知识点
16.已知直线









正确答案
4
解析
因为












考查方向
解题思路
结合直线与圆的相交关系构造半径,半弦长、圆心距之间的关系,求出参数m,然后结合平面几何知识求解。
易错点
直线与圆相交关系中的参数求解,圆的平面几何性质的应用。
知识点
19.如图,四棱锥










(I)证明

(II)求直线

正确答案
(Ⅰ)
由已知得







又




因为






解析
(Ⅰ)由已知得







又




因为





(Ⅱ)取






以










设




于是
考查方向
解题思路
1.结合线面平行的判定定理可证
2.建立直角坐标系
易错点
线面平行中平行关系的构造问题,利用平面法向量求面面角时注意法向量的正确运算,注意二面角是锐角还是钝角。
知识点
20. 已知抛物线








(I)若




(II)若


正确答案
(Ⅰ)
由于


记




所以
;(Ⅱ)
解析
由题设



记过



(Ⅰ)由于


记




所以
(Ⅱ)设


则
由题设可得


设满足条件的

当



而

当




考查方向
解题思路
设出与X轴垂直的直线,得出点的坐标,通过证明直线斜率即可证明结果
易错点
注意应用坐标法证明时利用斜率关系,求轨迹时不可忽视分类讨论。
知识点
17.已知数列


(1)证明
(2)若

正确答案
(Ⅰ)

解析
(Ⅰ)由题意得



由







因此



(Ⅱ)由(Ⅰ)得



解得
考查方向
1、数列通项与前项和为关系;2、等比数列的定义与通项及前项和为.
解题思路
通过变换结合等比数列的定义可证
利用等比数列定义建立方程
易错点
容易忘记验证n=1的成立性,等比数列求和公式应用出错。
知识点
18.下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图
(I)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(II)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量。
参考数据:


参考公式:相关系数
回归方程
正确答案
(Ⅰ)因为





解析
(Ⅰ)由折线图这数据和附注中参考数据得





因为





(Ⅱ)由


所以,


将2016年对应的

所以预测2016年我国生活垃圾无害化处理量将约1.82亿吨.
考查方向
解题思路
利用最小二乘法的原理提供的回归方程,准确求得相关数据即可建立回归方程做预测
易错点
最小二乘法的公式应用问题,数据的代入运算,相关系数的应用检测说明问题。
知识点
设函数



21.求
22.求A;
23.证明
正确答案
(Ⅰ)
解析
(Ⅰ)
考查方向
解题思路
(Ⅰ)直接可求
易错点
三角函数复合函数导数的求法;讨论含参数最值,对称轴与区间关系的分类分析;三角函数有界性与导数的分类讨论。
正确答案
Ⅱ
解析
(Ⅱ)当
因此,
当


令








令


(ⅰ)当






(ⅱ)当


又

综上,
考查方向
解题思路
(Ⅱ)分



易错点
三角函数复合函数导数的求法;讨论含参数最值,对称轴与区间关系的分类分析;三角函数有界性与导数的分类讨论。
正确答案
(Ⅲ)由(Ⅰ)得
当

当


当


解析
(Ⅲ)由(Ⅰ)得
当

当


当


考查方向
解题思路
(Ⅲ)首先由(Ⅰ)得到


易错点
三角函数复合函数导数的求法;讨论含参数最值,对称轴与区间关系的分类分析;三角函数有界性与导数的分类讨论。
请考生在选做题中任选一题作答。作答时用2B铅笔在答题卡上把所选题目题号后的方框涂黑。如果多做,则按所做的第一题计分。
24.选修4-1:几何证明选讲
如图,⊙O 中弧AB的中点为



(I)若

(II)若



25.选修4-4:坐标系与参数方程
在直角坐标系





(I)写出

(II)设点P在

26.选修4-5:不等式选讲
已知函数
(I)当a=2时,求不等式
(II)设函数



正确答案
(Ⅰ)










解析
(Ⅰ)连结

因为



又


(Ⅱ)因为









考查方向
解题思路
1、圆周角定理;2、三角形内角和定理;3、垂直平分线定理;4、四点共圆.
易错点
圆周角定理,四点共圆相关性质问题。
正确答案
(Ⅰ)




解析
选修4-4:坐标系与参数方程
(Ⅰ)



(Ⅱ)由题意,可设点



即为



………………8分
当且仅当




考查方向
1、椭圆的参数方程;2、直线的极坐标方程.
解题思路
利用同角三角函数关系中的平方关系化曲线c1 的参数方程 普通方程式,利用公式代入C2的极坐标方程即可
易错点
参数方程与普通方程的互化,点线距中最后与三角的综合应用。
正确答案
(Ⅰ)

解析
(Ⅰ)当

解不等式

因此,

(Ⅱ)当

当
所以当


当

当


所以

考查方向
解题思路
(Ⅰ)利用等价不等式


易错点
绝对值符号的去掉讨论,含参数问题的分类讨论。