理科数学成都市2015年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共10小题，每小题5分，共50分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

1．已知为虚数单位，，若为纯虚数，则复数的模等于（　　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

虚数单位i及其性质

题型：单选题

分值: 5分

3．某几何体正视图与侧视图相同，其正视图与俯视图如图所示，且图中的四边形都是边长为2的正方形，正视图中两条虚线互相垂直，则该几何体的体积是（　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

分值: 5分

2．如图所示的程序框图的输入值，则输出值的取值范围为（　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

顺序结构

题型：单选题

分值: 5分

5．已知等比数列的前n项和为，且，，则（　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等比数列的性质及应用

题型：单选题

分值: 5分

7．若正实数，满足，则的最大值是( 　 )

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：单选题

分值: 5分

9．定义在上的函数,是它的导函数,且恒有成立,则（　　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

题型：单选题

分值: 5分

10．已知R上的连续函数g(x)满足：

①当时，恒成立(为函数的导函数)；

②对任意的都有，又函数满足：对任意的，都有成立。

当时，。若关于的不等式对恒成立,则的取值范围是（　）

D或

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二项式定理的应用

题型：单选题

分值: 5分

4．下列命题正确的个数是（　）

①“在三角形中，若,则”的逆命题是真命题；

②命题或，命题则是的必要不充分条件；

③“”的否定是“”；

④若随机变量，则

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：单选题

分值: 5分

6．若函数的图像向右平移个单位后与原函数的图像关于轴对称，则的最小正值是（　　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两圆的公切线条数及方程的确定

题型：单选题

分值: 5分

8．某校周四下午第三．四两节是选修课时间,现有甲、乙、丙、丁四位教师可开课。已知甲、乙教师各自最多可以开设两节课,丙、丁教师各自最多可以开设一节课，现要求第三、四两节课中每节课恰有两位教师开课(不必考虑教师所开课的班级和内容),则不同的开课方案共有（　　）种。

A20

B19

C16

D15

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

圆系方程

填空题本大题共5小题，每小题5分，共25分。把答案填写在题中横线上。

题型：填空题

分值: 5分

11．已知函数，则的解集为．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

诱导公式的推导

题型：填空题

分值: 5分

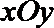
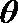
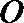
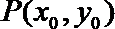
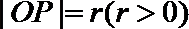
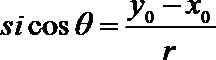
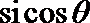
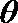
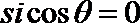
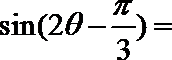
13．在直角坐标系中，已知任意角以坐标原点为顶点，以轴的非负半轴为始边，若其终边经过点，且，定义：，称“”为“的正余弦函数”，若，则．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平行公理

题型：填空题

分值: 5分

14．如图，四边形是边长为1的正方形，延长至，使得。动点从点出发，沿正方形的边按逆时针方向运动一周回到点，．则的取值范围为．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：填空题

分值: 5分

15．在实数集R中，我们定义的大小关系“＞”为全体实数排了一个“序”．类似的，我们在平面向量集上也可以定义一个称“序”的关系，记为“”．定义如下：对于任意两个向量，“”当且仅当“”或“”。按上述定义的关系“”，给出如下四个命题：

①若，则；

②若，则；

③若，则对于任意；

④对于任意向量，若，则。

其中真命题的序号为。

正确答案

①②③

解析

解析已在路上飞奔，马上就到！

知识点

平面向量数量积的坐标表示、模、夹角

题型：填空题

分值: 5分

12．的展开式中各项系数的和为2，则该展开式中常数项为．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

简答题（综合题）本大题共75分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

17．如图，海上有两个小岛相距10，船O将保持观望A岛和B岛所成的视角为，现从船O上派下一只小艇沿方向驶至处进行作业，且．设。

（1）用分别表示和，并求出的取值范围；

（2）晚上小艇在处发出一道强烈的光线照射A岛，B岛至光线的距离为，求BD的最大值．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的几何意义

题型：简答题

分值: 12分

18．在四棱锥中，，，点是线段上的一点，且，．

（1）证明：面面；

（2）求直线与平面所成角的正弦值．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：简答题

分值: 12分

19．某重点大学自主招生考试过程依次为自荐材料审查．笔试．面试共三轮考核。规定：只能通过前一轮考核才能进入下一轮的考核，否则将被淘汰；三轮考核都通过才算通过该高校的自主招生考试。学生甲三轮考试通过的概率分别为，，，且各轮考核通过与否相互独立。
（1）求甲通过该高校自主招生考试的概率；
（2）若学生甲每通过一轮考核，则家长奖励人民币1000元作为大学学习的教育基金。记学生甲得到教育基金的金额为，求的分布列和数学期望。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：简答题

分值: 12分

16．集合，，若命题，命题，且是必要不充分条件，求实数的取值范围。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

题型：简答题

分值: 14分

21．设函数,．

（1）求的极大值；

（2）求证：

（3）当方程有唯一解时，试探究函数与的图象在其公共点处是否存在公切线，若存在．研究的值的个数；若不存在，请说明理由．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：简答题

分值: 13分

20．已知数列中,且点在直线上。

（1）求数列的通项公式；

（2）若函数求函数的最小值；

（3）设表示数列的前项和．试问:是否存在关于的整式,使得

对于一切不小于2的自然数恒成立？若存在，写出的解析式，并加以证明；若不存在,试说明理由。

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷