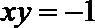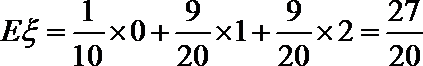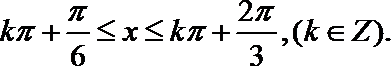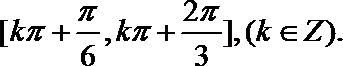- 真题试卷
- 模拟试卷
- 预测试卷
2.已知复数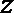
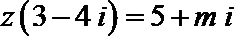
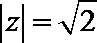
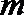
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.由


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.如果执行下面的程序框图,那么输出的
正确答案
2009
解析
解析已在路上飞奔,马上就到!
知识点
6.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数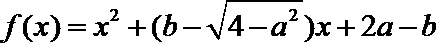

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知对任意平面向量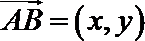
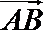
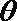


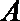


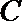
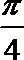

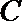
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.过点







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若对任意的实数

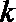
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.在棱锥






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.在正项等比数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.对任意







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在平面直角坐标系中,定义
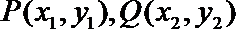
① 到原点的“折线距离”等于1的点的集合是一个正方形;
② 到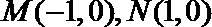
③ 到
④ 到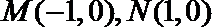
其中正确的命题是____________(写出所有正确命题的序号)
正确答案
①③④
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.点









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
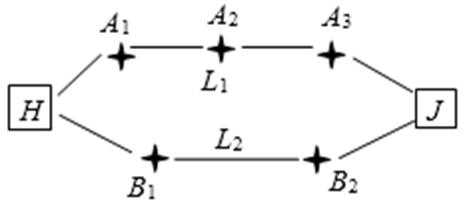
20.高山先生家住
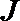
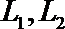
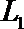
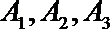


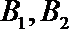


(1)若走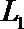
(2)若走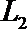
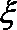
正确答案
(1)设走L1路线最多遇到1次红灯为A事件,则
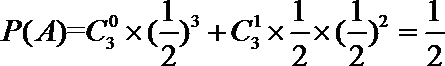
所以走L1路线,最多遇到1次红灯的概率为
(2)依题意,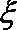

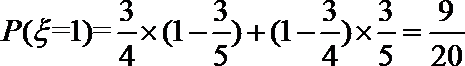
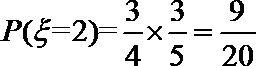
随机变量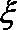
解析
解析已在路上飞奔,马上就到!
知识点
22.已知双曲线














(1)求双曲线的方程;
(2)判断
(3)求三角形
正确答案
(1)双曲线的方程为
(2)由(1)可知

所以设直线



设

由韦达定理知
所以
因为
向量

(3)因为直线

所以


令

又



解析
解析已在路上飞奔,马上就到!
知识点
21.如图,正三棱柱



(1)求异面直线

(2)求证:

(3)求点

正确答案
(1)
(2)取






平面



连结





在正方形

又



(3)


在正三棱柱中,


设点


由


∴点


解析
解析已在路上飞奔,马上就到!
知识点
23.已知




(1)求



(2)已知










(3)在(2)的条件下,设

正确答案
(1)∵点


又



①当



②当



=



(2)由(1)知,当

∴

∴





①+②得,

又








∴


当



(3)

将所得的积排成如下矩阵:

设矩阵

在矩阵的左下方补上相应的数可得
矩阵

矩阵

………
矩阵


从而矩阵

所以
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知函数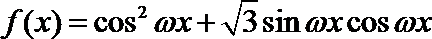
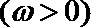
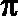
(1)若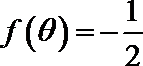
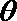
(2)求函数
正确答案
(1) 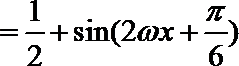
因为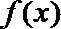
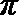

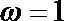
由题意得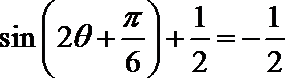

所以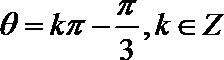
(2)分别由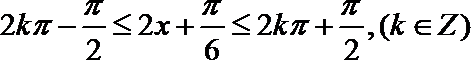
可得
所以,函数
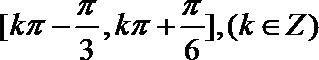
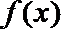
由
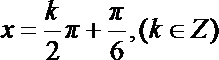
所以,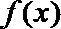
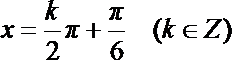
解析
解析已在路上飞奔,马上就到!