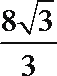- 真题试卷
- 模拟试卷
- 预测试卷
3.设函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设i=(1,0),j=(0,1),若向量a满足|a-2i|+|a-j|=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知实数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 设集合A={x|


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
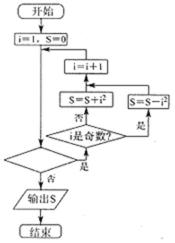
4. 执行如图中的程序框图,若输出的结果为21,则判断框中应填( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知各项为正数的等差数列

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 已知双曲线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.如图,在三棱锥










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
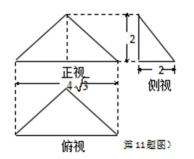
11.已知某几何体的三视图如图所示,则该几何体的体积是___________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.如图,在正方形ABCD中,E为AB的中点,P为以A为圆心, AB为半径的圆弧上的任意一点,设向量

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 在一个人数很多的团体中普查某种疾病,为此要抽N个人的血,可以用两种方法进行.
(1)将每个人的血分别去验,这就需N次.
(2)按k个人一组进行分组,把从k个人抽出来的血混在一起进行检验,如果这混合血液呈阴性反应,就说明k个人的血液都呈阴性反应,这样,这k个人的血就只需验一次.若呈阳性,则再对这k个人的血液分别进行化验.这样,这k个人的血总共要化验k+1次.假设每个人化验呈阳性的概率为p,且这些人的试验反应是相互独立的.
(Ⅰ)设以k个人为一组时,记这k个人总的化验次数为X,求X的分布列与数学期望;
(Ⅱ)设以k个人为一组,从每个人平均需化验的次数的角度说明,若

正确答案
(Ⅰ)
(Ⅱ)即


且

解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,


(1)求证:直线CD的斜率为定值;
(2)延长DC交x轴负半轴于点E,若EC : ED = 1 : 3,求
正确答案
解:(1)将点(1,1)代入

设

联立得:


由题意有

(2)设



同理

∴

因此:
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(Ⅰ)求函数
(Ⅱ) 已知

正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,斜三棱柱




(Ⅰ )证明:


(Ⅱ )在平面


正确答案
解:(Ⅰ )面





所以

取















在

取




(Ⅱ )在


则因为



在













该点即为所求,且


解析
解析已在路上飞奔,马上就到!
知识点
20. 已知函数


(Ⅰ)求实数
(Ⅱ)当


(Ⅲ)试证明:
正确答案
解:(Ⅰ)


(Ⅱ)当
由

取
再取
故

而
故


故


(Ⅲ)由(Ⅱ)知:
令


解析
解析已在路上飞奔,马上就到!
知识点
21. 若函数










(1)对任意

(2)求证: 
(3)求证:存在唯一实数

正确答案
证明(1)


(2) 由第(1)题结论知:








(3)记



即









假设还存在另一个实数










解析
解析已在路上飞奔,马上就到!