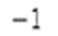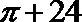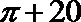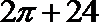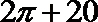- 真题试卷
- 模拟试卷
- 预测试卷
2. 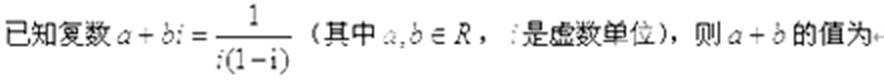
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
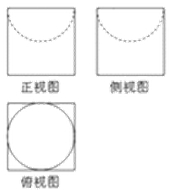
6.如图是一个无盖器皿的三视图,正视图、侧视图和俯视图中的正方形边长为2,正视图、侧视图中的虚线都是半圆,则该器皿的表面积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
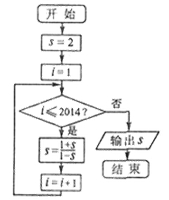
9. 某程序框图如图所示,该程序运行后输出的
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 已知实数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知角



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则图中的
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.下列四个函数中,既是定义域上的奇函数又在区间
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知三棱锥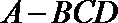
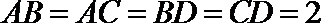
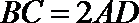
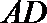
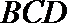
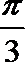
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知直线








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 某工厂生产






正确答案
80
解析
解析已在路上飞奔,马上就到!
知识点
14. 若正数


正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
16.设圆



使得

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知各项均为正数的数列




(1)求数列
(2)令



正确答案
(1)由已知

两式相减,得
又

当



(2)

由①

由①-②得
解析
解析已在路上飞奔,马上就到!
知识点
19. 某工厂生产

(1)试依据以频率估计概率的统计思想,分别估计元件

(2)生产一件元件

(i)记



(ii)求生产5件元件
正确答案
(1)原件
原件
(2)(i)随机变量





所以,随机变量

(ii)设生产的5件元件


以题意,得

所以,
设“生产5件元件
解析
解析已在路上飞奔,马上就到!
知识点
20. 如图,在三棱锥










(1)求证:

(2)当

正确答案

在



(2)解法二:如图,以





设



设平面
则

令

由(1)可知




解析
解析已在路上飞奔,马上就到!
知识点
21. 已知




(1)求曲线
(2)过











正确答案
(1)设

由余弦定理得
即
又

由于
因此点



所以,曲线

解析
解析已在路上飞奔,马上就到!
知识点
17.已知
(1)求
(2)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22. 已知函数



(1)求函数
(2)若不等式


正确答案
(1)








令


当




当




故


(2)原不等式等价于:

设
则
令
①




不符合题意,舍去.
②当
则



不符合题意,舍去.
解析
解析已在路上飞奔,马上就到!