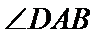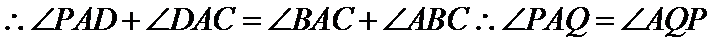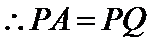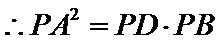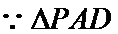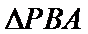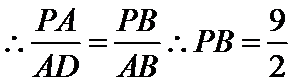- 真题试卷
- 模拟试卷
- 预测试卷
1.设集合

正确答案
解析
集合A中的不等式可化为


则
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
分别求解不等式得到
再借助数轴进行交集运算,即可得到结果。
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
如何把不等号两边化为“同底”
解对数不等式时忽略了真数大于0
知识点
4.口袋
正确答案
解析
记取到的两个球都是白球为事件A, 取到的两个球同色为事件B
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
利用
易错点
在利用公式计算条件概率时,在条件发生的前提下,样本容量已经发生改变。
知识点
5.已知



正确答案
解析
可行域
把目标函数化为直线的斜截式





A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
解题思路
可变为
A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
可行域和目标函数对应的直线的画图出现错误

知识点
8.已知函数



正确答案
解析
已知函数

得
所以,
B选项不正确,C选项不正确,D选项不正确,所以选A选项。
考查方向
解题思路
把点P代入
结合图像可知
B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
对于方程
知识点
9.等腰直角










所在圆的半径)
正确答案
考查方向
解题思路
1.水平方向及直角边上运动时,圆心是呈直线运动的
易错点
圆
知识点
10.已知数列




正确答案
考查方向
解题思路
1. 分析


易错点
不能定量分析

知识点
2. 设命题











正确答案
解析
命题P中,当


命题Q中,因为







A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
分别判断命题
利用含有“或、且、非”命题的真假的判断方法,即可得到结果。
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
命题P的真假判断时容易忽略
不能理解不等式
知识点
3.已知复数
正确答案
解析

B选项不正确,C选项不正确,D选项不正确,所以选A选项。
考查方向
解题思路
先计算
再计算
B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点

知识点
6.如图,给出的是求

则判断框内填入的条件是
正确答案
解析
当



以此类推,当




A选项不正确,C选项不正确,D选项不正确,所以选B选项。
考查方向
解题思路
当



以此类推,当




易错点
没看清“是”,“否”,不等号方向写反,本题循环结构为
当型循环,当满足条件时执行循环体,因此排除A,D项;
求和后,




知识点
7. 在平面直角坐标系中,双曲线




正确答案
解析
设双曲线的标准方程为
又因为点

所以,所求双曲线的标准方程我
考查方向
解题思路
采用待定系数法,由由双曲线的渐近线设标准方程
把点P代入方程求解,即可得到结果。
易错点
由双曲线的渐近线设标准方程出错
知识点


则正方形

正确答案
解析
可求得正方形









A选项不正确,C选项不正确,D选项不正确,所以选B选项。
考查方向
解题思路
求出球心到正方形的中心的距离,再结合图形判断位置关系求解.
易错点
球心位置的确定
知识点
12.已知点




正确答案
解析
.设
令
令




所以, 

则线段
A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
解题思路
设
P到圆心距离的最小值减去圆的半径即为所求。
易错点
不能找到正确的解题思路
知识点
13.若

正确答案
-1
解析

当

考查方向
解题思路
运用微积分基本定理,求出m
当x=1,所有二项式的值即为展开式的系数和
易错点
求错原函数。 二项式的展开式的二项系数和与系数和混淆
知识点







正确答案
考查方向
解题思路
1. 运用B,C,P共线,则
易错点
不能利用m与n的关系建立动点横坐标x与纵坐标y之间的联系。
知识点
15.数列





正确答案
考查方向
解题思路
1. 当
易错点
当

知识点
16.一个空间几何体的三视图如图所示,
则这个几何体的体积为 .
正确答案
考查方向
易错点

.
23.求抛物线
24.已知动圆







正确答案
(1)
解析
(1) 设抛物线的焦点为

由







考查方向
解题思路
联立直线与抛物线方程,求解抛物线过焦点的弦长.
设动圆圆心

易错点
联立消元计算出错
第2问计算量较大,对学生的运算能力是个严重的考验。
不能正确地两次利用基本不等式求最值。
正确答案
(2)
解析
设动圆圆心

且圆
令

解得:
设
当

当





综上①知



当且仅当

所以

考查方向
解题思路
联立直线与抛物线方程,求解抛物线过焦点的弦长.
设动圆圆心

易错点
联立消元计算出错
第2问计算量较大,对学生的运算能力是个严重的考验。
不能正确地两次利用基本不等式求最值。
已知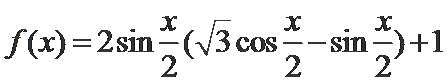
17.若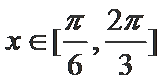
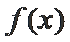

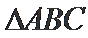
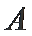
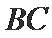
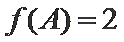
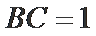
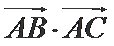
正确答案
(1)值域为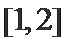
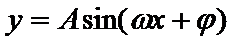
解析
(Ⅰ)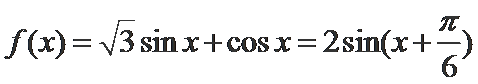

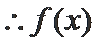
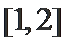
解题思路
利用降幂公式、辅助角公式把函数化成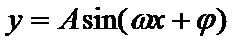
利用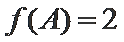
易错点
求值域时,直接带定义域的端点求最值
第2问没能联想到基本不等式求最值。
正确答案
最大值为
解析
(Ⅱ)
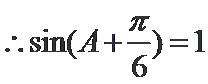
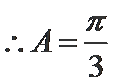
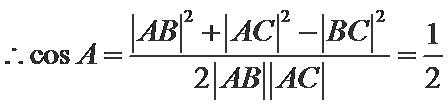
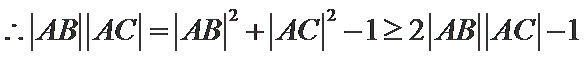
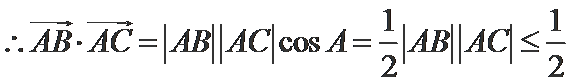
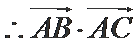
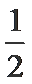
考查方向
解题思路
利用降幂公式、辅助角公式把函数化成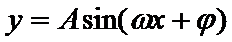
利用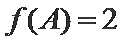
易错点
求值域时,直接带定义域的端点求最值
第2问没能联想到基本不等式求最值。
某汽车公司为调查4S店个数对该
19.根据该统计数据进行分析,求y关于x的线性回归方程;
20.现要从A,B,E三座城市的9家4S店中选取4家做深入调查,求A城市中
被选中的4S店个数X的分布列和期望.
附:回归直线的斜率和截距的最小二乘法估计公式分
, .
正确答案
(1)
解析
(Ⅰ)




考查方向
解题思路
带公式求线性回归方程;
先找出随机变量的所有取值,分别求对应的概率并列出表格,然后到公式求出期望。
易错点
带公式求方程计算出错
分布列中随机变量求值及其概率求错
正确答案
(2)
解析






-------------9分

考查方向
解题思路
带公式求线性回归方程;
先找出随机变量的所有取值,分别求对应的概率并列出表格,然后到公式求出期望。
易错点
带公式求方程计算出错
分布列中随机变量求值及其概率求错
正方体





21.当


22.当平面



正确答案
(1)证明略;(2)
解析




正方体









考查方向
解题思路
利用线面垂直的判定定理及线面垂直的定义求证第1问
建立适当的空间直角坐标系,利用空间向量求解二面角的余弦值
易错点
平面的法向量计算出错
正确答案
(2)
解析
正方体



分别以





设







则



平面

平面







设平面


则
考查方向
解题思路
利用线面垂直的判定定理及线面垂直的定义求证第1问
建立适当的空间直角坐标系,利用空间向量求解二面角的余弦值
易错点
平面的法向量计算出错
已知函数




25.若函数

26.当(Ⅰ)中的

正确答案
解析
(1)解:
①



而

故

②





令



若

若


又
令

令



令



故


则
故


综上,

考查方向
解题思路
利用导数讨论函数的单调性与极值,并与图像结合。
利用第一问的结论化简左边的函数式,然后讨论函数的单调性和极值,即可得到结果。
易错点
忽视了函数的定义域
第一问中没有对k进行分类讨论
第二问的证明过程中不能正确利用第一问的结论化简函数。
正确答案
证明略
解析
由(1)知,


而

则

记

令



而



即
则





则


故

故
考查方向
解题思路
利用导数讨论函数的单调性与极值,并与图像结合。
利用第一问的结论化简左边的函数式,然后讨论函数的单调性和极值,即可得到结果。
易错点
忽视了函数的定义域
第一问中没有对k进行分类讨论
第二问的证明过程中不能正确利用第一问的结论化简函数。
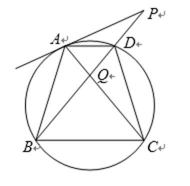
等腰梯形

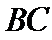

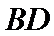


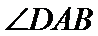
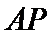
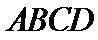
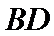

27.求证: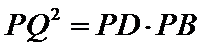
28.若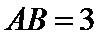

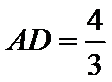

正确答案
(1)证明略;
解析
(1) 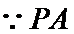

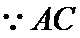
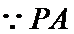

考查方向
解题思路
根据切割线定理得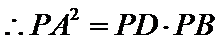
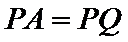
根据同弧对的圆周角相等,可得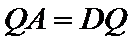
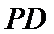
易错点
难以找出相等的角,进而将边转化求长度.
正确答案
解析


考查方向
解题思路
根据切割线定理得
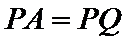
根据同弧对的圆周角相等,可得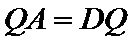

易错点
难以找出相等的角,进而将边转化求长度.