- 真题试卷
- 模拟试卷
- 预测试卷
1.复数



正确答案
解析

知识点
3.已知集合

正确答案
解析
集合A是圆


知识点
5.如图3,



正确答案
解析

知识点
7.



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 定义某种运算

正确答案
解析

知识点
8.如下图:(1)是反映某条公共汽车线路收支差额(即营运所得票价收入与付出成本的差)

给出下说法:
①图(2)的建议是:提高成本,并提高票价;
②图(2)的建议是:降低成本,并保持票价不变;
③图(3)的建议是:提高票价,并保持成本不变;
④图(3)的建议是:提高票价,并降低成本.
其中所有说法正确的序号是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.为了解某商品销售量y(件)与销售价格x(元/件)的关系,统计了(x,y)的10组值,并画成散点图如图,则其回归方程可能是( )
正确答案
解析
由散点图可知商品销售量y(件)与销售价格x(元/件)具有负线性相关的关系,易知选B.
知识点
4.如图2,正三棱柱
正确答案
解析
其侧视图是长
知识点
11.已知定义在R上的奇函数




正确答案
0
解析


知识点
9.已知等差数列

正确答案
14
解析
知识点
10.已知函数
正确答案
解析





知识点
12.若点P在曲线C1:
正确答案
10
解析
由双曲线定义可得:(| PQ |-| PR | )max=
知识点
选做题14、15题选做一题,若两题都作答,只按第一题评分.
14.(极坐标、参数方程选做题)
⊙O1和⊙O2的极坐标方程分别
15.(几何证明选讲选做题)
如图,MN是圆O的直径,MN的延长线与圆O上过点P的切线PA相交于点A,若

正确答案
14.
15. 4
解析
14.两个圆的直角坐标方程为

15.
知识点
13.一科研人员研究








①
②若今天的



③假设科研人员将

其中正确的序号为___________ .
正确答案
③
解析
解析已在路上飞奔,马上就到!
知识点
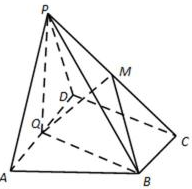
18.如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
(1)若点M是棱PC的中点,求证:PA // 平面BMQ;
(2)求证:平面PQB⊥平面PAD;
(3)若二面角M-BQ-C为30°,设PM=tMC,试确定t的值 .
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.定义:设函数y=f(x)在(a,b)内可导,
(1)证明函数

(2)对



(3)当n为正整数时,定义函数N (n)表示n的最大奇因数.如N (3) = 3,N (10) = 5,….记



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17、某公司准备将100万元资金投入代理销售业务,现有A,B两个项目可供选择:
投资A项目一年后获得的利润X1(万元)的概率分布列如下表所示:
且X1的数学期望E(X1)=12;
投资B项目一年后获得的利润X2(万元)与B项目产品价格的调整有关, B项目产品价格根据销售情况在4月和8月决定是否需要调整,两次调整相互独立且在4月和8月进行价格调整的概率分别为p(0< p <1)和1p. 经专家测算评估:B项目产品价格一年内调整次数X(次)与X2的关系如下表所示:
(1)求a,b的值;
(2)求X2的分布列;
(3)若E(X1)< E(X2),则选择投资B项目,求此时 p的取值范围.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知定义在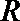
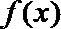
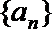
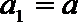
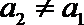
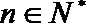
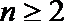
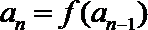
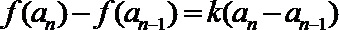
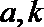
(1)若数列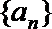
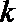
(2)令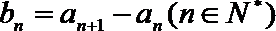
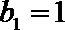
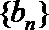
(3)试研究数列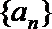
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知向量


(1)求角A的大小;
(2)若BC=2,求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图所示,



(1)求抛物线方程;
(2)已知过点
















正确答案
解析
解析已在路上飞奔,马上就到!