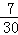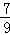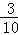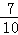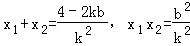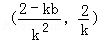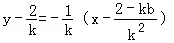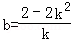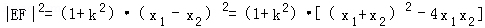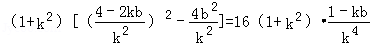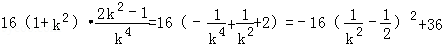- 真题试卷
- 模拟试卷
- 预测试卷
2.给出下列四个命题:命题p1:“a=0,b≠0”是“函数y=x2+ax+b为偶函数”的必要不充分条件;命题p2:函数
正确答案
解析
略。
知识点
4.已知m、n是两条不同的直线,α、β、γ是三个不同的平面,则下列命题正确的是( )
正确答案
解析
略。
知识点
7.过双曲线



正确答案
解析
略。
知识点
1.设复数z满足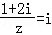
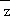
正确答案
解析
略。
知识点
3.已知集合A={x|x2﹣x﹣2<0},B={x|y=lg
正确答案
解析
略。
知识点
5.①从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
②若两个随机变量的线性相关性越强,则相关系数的绝对值越接近于1;
③根据散点图求得的回归直线方程可能是没有意义的;
④若某项测量结果ξ服从正态分布N(1,σ2),且P(ξ≤4)=0.9,则P(ξ≤﹣2)=0.1。
其中真命题的个数为( )
正确答案
解析
略。
知识点
8.已知函数若x,y满足约束条件
正确答案
解析
略。
知识点
6.10件产品中有3件次品,不放回地抽取2次,在第1次抽出的是次品的前提下,则第2次抽出正品的概率是( )
正确答案
解析
略。
知识点
9.已知一个四位数其各个位置上的数字是互不相等的非负整数,且各个数字之和为12,则这样的四位数的个数是( )
正确答案
解析
略。
知识点
10.定义:如果函数f(x)在[a,b]上存在x1,x2(a<x1<x2<b),满足f′(x1)=


正确答案
解析
略。
知识点
15.直线l的参数方程是

正确答案
2
解析
略。
知识点
13.(1+x)(1﹣x)10 展开式中x3的系数为_______。
正确答案
-75
解析
略。
知识点
14.意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一列数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和,人们把这样的一列数所组成的数列{an}称为“斐波那契数列”。那么
正确答案
2016
解析
略。
知识点
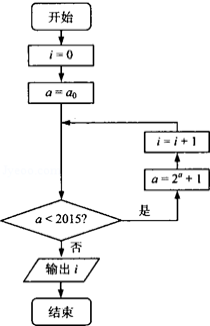
12.执行如图所示的程序框图,若输出结果是i=3,则正整数a0的最大值为_______。
正确答案
3
解析
略。
知识点
16.在极坐标系中,点P(2,﹣

正确答案
3
解析
略。
知识点
11.已知tanβ=

正确答案
解析
略。
知识点
17.设函数f(x)=sin2x+cos(2x+
(1)求函数f(x)的最大值及此时x的取值集合;
(2)设A,B,C为△ABC的三个内角,若cosB=


正确答案
(1)f(x)max=

(2)sinA=
解析
(1)f(x)=




∴当sin2x=﹣1时,
f(x)max=
此时2x=2kπ﹣
∴x的取值集合为{x|x=kπ﹣
(2)∵f(



∴sinC=
∵C为锐角,
∴C=
由cosB=


∴sinA=sin(


知识点
18.一个盒子里装有7张卡片,其中有红色卡片4张,编号分别为1,2,3,4; 白色卡片3张,编号分别为2,3,4.从盒子中任取4张卡片 (假设取到任何一张卡片的可能性相同)。
(1)求取出的4张卡片中,含有编号为3的卡片的概率;
(2)再取出的4张卡片中,红色卡片编号的最大值设为X,求随机变量X的分布列和数学期望。
正确答案
见解析。
解析
(1)设取出的4张卡片中,含有编号为3的卡片为事件A,则
P(A)=
所以,取出的4张卡片中,含有编号为3的卡片的概率为
(2)随机变量X的所有可能取值为1,2,3,4
P(X=1)=
P(X=3)=


EX=
X的分布列为
知识点
19.已知{an}是由正数组成的数列,其前n项和Sn与an之间满足:an+

(1)求数列{an}的通项an;
(2)设bn=(
正确答案
(1)an=n
(2)Tn=
解析
(1)∵an+

∴
当n≥2时,
∴an=Sn﹣Sn﹣1=

化为(an+an﹣1)(an﹣an﹣1﹣1)=0,
∵an+an﹣1>0,∴an﹣an﹣1=1,
∴数列{an}为等差数列,
∴an=1+(n﹣1)×1=n
(2)bn=

∴数列{bn}的前n项和Tn=

∴


∴




∴Tn=1+




知识点
如图,在三棱锥P﹣ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连结GH。
(1)求证:AB∥GH;
(2)求平面PAB与平面PCD所成角的正弦值。
正确答案
见解析。
解析
(1)证明:∵D,C,E,F分别是AQ,BQ,AP,BP的中点,
∴EF∥AB,DC∥AB,
∴EF∥DC
又EF⊄平面PCD,DC⊂平面PCD,
∴EF∥平面PCD
又EF⊂平面EFQ,平面EFQ∩平面PCD=GH,
∴EF∥GH
又EF∥AB,
∴AB∥GH
(2)解:在△ABQ中,∵AQ=2BD,AD=DQ,∴∠ABQ=90°,即AB⊥BQ。
又PB⊥平面ABQ,∴BA,BQ,BP两两垂直。
以B为坐标原点,分别以BA,BQ,BP所在直线为x轴,y轴,z轴,
建立如图所示的空间直角坐标系。设BA=BQ=BP=2,
则B(0,0,0),Q(0,2,0),D(1,1,0),
C(0,1,0),P(0,0,2),
∴

设平面PCD的一个法向量为
由





又
∴cos<n,

设平面PAB与平面PCD所成角为θ,
则sinθ=

故平面PAB与平面PCD所成角的正弦值为
知识点
21.已知定点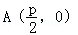
(I)求动点M的轨迹C的方程;
(2)设EF为曲线C的一条动弦(EF不垂直于x轴),其垂直平分线与x轴交于点T(4,0),当p=2时,求|EF|的最大值。
正确答案
(1)y2=2px(p>0,x≠0)
(2)|EF|的最大值为6
解析
如图,
(1)设M(x,y),则BM的中点G的坐标为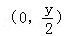
又A(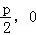
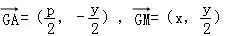
由题意知GA⊥GM,所以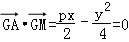
所以y2=2px
当M点在x轴上时不满足题意,故曲线C的方程为y2=2px(p>0,x≠0);
(2)设弦EF所在直线方程为y=kx+b,E(x1,y1),F(x2,y2)
由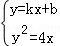
则
则线段EF的中点为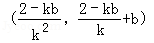
线段EF的垂直平分线方程为
令y=0,x=4,得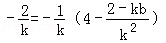
所以
=
=
再由①,△=(2kb﹣4)2﹣4k2b2=4k2b2﹣16kb+16﹣4k2b2=16﹣16kb
=16﹣16(2﹣2k2)=32k2﹣16>0
得: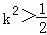
所以,当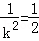
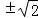
知识点
22.已知函数f(x)=ax+
(1)若f(x)≥lnx在[1,+∞)上恒成立,求a的取值范围;
(2)证明:1+



(3)已知S=1+


正确答案
见解析。
解析
(1)∵函数f(x)=ax+
f(x)≥lnx在[1,+∞)上恒成立,
设g(x)=f(x)﹣lnx,则g(x)=f(x)﹣lnx≥0在[1,+∞)上恒成立,
∴g(x)min≥0,
又∵g′(x)=a﹣


而当

①当

g′(x)≥0在[1,+∞)上恒成立,
∴g(x)min=g(1)=0≥0;
②当

g′(x)=0时x=
且1≤x<
当x>
则g(x)min=g(
又∵g(
∴综上所述,a的取值范围为:[
(2)证明:由(1)可知a
则当a=


令x依次取



则有 







… 



由同向不等式可加性可得









即 







也即 




也即1+



(3)由(2)的结论,可得,S=1+



又S=1+




则有S的整数部分为9。