理科数学衡水市2014年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

1.设集合M={x|x2≤4），N={x|log2 x≥1}，则M∩N等于（　　）

A[﹣2，2]

B{2}

C[2，+∞）

D[﹣2，+∞）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

简单复合函数的导数

题型：单选题

分值: 5分

2.若、，则是的( )

A充分非必要条件

B必要非充分条件

C充要条件

D非充分非必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

3.平面直角坐标系xOy中，已知A(1,0)，B（0,1），点C在第二象限内，，且|OC|=2，若，则，的值是（）

A，1

B1，

C-1，

D，1

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

12．设定义域为的函数若关于的方程有7个不同的实数解，则= （）

B4或6

C2或6

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

9．已知各项均为正数的等比数列满足,若存在两项使得的最小值为（　　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等比数列的基本运算等比数列的性质及应用利用基本不等式求最值

题型：单选题

分值: 5分

4.设是公差不为0的等差数列的前n项和，且成等比数列，则的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：单选题

分值: 5分

5．如图，圆O的两条弦AB和CD交于点E，EF//CB,EF交AD的延长线于点F，FG切圆O于点G，EF=2，则FG的长为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

6．某四棱锥的三视图如图所示，则最长的一条侧棱的长度是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

题型：单选题

分值: 5分

8．已知为互不相等的正数，，则下列关系中可能成立的是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

11．若函数，

（其中且），则下列选项中一定是方程的根的是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

题型：单选题

分值: 5分

7．已知、是两条不同的直线,、是两个不同的平面,给出下列命题

①若,则;

②若,且则;

③若,则;

④若,,且,则.

其中正确命题的个数是（　　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：单选题

分值: 5分

10．已知关于的一元二次不等式的解集中有且仅有3个整数，则所有符合条件的值之和是（）

A13

B18

C21

D26

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

填空题本大题共4小题，每小题5分，共20分。把答案填写在题中横线上。

题型：填空题

分值: 5分

13．若,且,则 ___________.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 5分

15.已知函数若使得，则实数的取值范围是___________.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：填空题

分值: 5分

16．设关于x,y的不等式组表示的平面区域内存在点P(x0，y0)满足x0－2y0=2，则m的取值范围是___________.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：填空题

分值: 5分

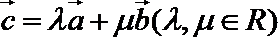
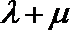
14．向量a，b，c在正方形网格中的位置如图所示，若，则=__________.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平面向量的基本定理及其意义

简答题（综合题）本大题共70分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

20．已知分别在射线（不含端点）上运动，，在中，角、、所对的边分别是、、．

（Ⅰ）若、、依次成等差数列，且公差为2．求的值；

（Ⅱ）若，，试用表示的周长，

并求周长的最大值．

正确答案

（Ⅰ）、、成等差，且公差为2，

、. 又，，

，，

恒等变形得，解得或.又，.

（Ⅱ）在中，，，，.

的周长

，

又，,

当即时，取得最大值．

解析

解析已在路上飞奔，马上就到！

知识点

一元二次不等式的解法

题型：简答题

分值: 12分

21．已知函数．

（I）讨论的单调性；

（II）若恒成立，证明：当时，．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

题型：简答题

分值: 12分

17．在三棱柱中，侧面为矩形，，为的中点，与交于点，侧面．

（1）证明：;

（2）若，求三棱锥的体积。

正确答案

（1）根据题意，由于在三棱柱中，

侧面为矩形，

，为的中点，与交于点，侧面，

那么在底面Z中，利用相似三角形可知，,,

进而得到,则可知;

（2）如果，那么利用，为的中点，

勾股定理可知,根据柱体的高，以及底面积可知三棱柱的体积为

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：简答题

分值: 12分

18．已知函数在（0，1）上是增函数，

（1）实数m的取值集合为A，当m取集合A中的最小值时，定义数列满足且，求数列{an}的通项公式；

（2）若,数列的前n项和为，求证：.

正确答案

（1）由题意得f′（x）=﹣3x2+m，

∵f（x）=﹣x3+mx在（0，1）上是增函数，

∴f′（x）=﹣3x2+m≥0在（0，1）上恒成立，

即m≥3x2，得m≥3，

故所求的集合A为[3，+∞）

所以m=3，∴f′（x）=﹣3x2+3，

∵，an＞0，∴=3an，即=3，

∴数列{an}是以3为首项和公比的等比数列，故an=3n；

（2）由（1）得，bn=nan=n•3n，

∴Sn=1•3+2•32+3•33+…+n•3n ①

3Sn=1•32+2•33+3•34+…+n•3n+1 ②

① ﹣②得，﹣2Sn=3+32+33+…+3n﹣n•3n+1=﹣n•3n+1

化简得，Sn=＞．

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：简答题

分值: 12分

19.某工厂某种产品的年固定成本为250万元，每生产千件，需另投入成本为，当年产量不足80千件时，（万元）.当年产量不小于80千件时，（万元）.每件商品售价为500元.通过市场分析，该厂生产的商品能全部售完.

（Ⅰ）写出年利润（万元）关于年产量（千件）的函数解析式；

（Ⅱ）年产量为多少千件时，该厂在这一商品的生产中所获利润最大？

正确答案

（Ⅰ）

为1000万元.

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的图像

题型：简答题

分值: 10分

请考生在第（22）、（23）两题中任选一题作答。注意：只能做所选定的题目。如果多做，则按所做的第一个题目计分。

22．如图，AB是圆O的直径，C是半径OB的中点，D是OB延长线上一点，且BD=OB，直线MD与圆O相交于点M、T，（不与a、b重合），DN与圆O相切于点N，连结MC，MB，OT。

（I）求证：；

（II）若，试求的大小。

23．已知函数．

（I）解不等式；

（II）若，求证：≤.

正确答案

22.（1）证明：因MD与圆O相交于点T，由切割线定

理，，得

，设半径OB=，因BD=OB，且BC=OC=，

则，，

所以

（2）由（1）可知，，且，

故∽，所以；

根据圆周角定理得，，则

23.（1）由题.

因此只须解不等式.

当时，原不式等价于，即.

综上,原不等式的解集为.

（2）由题.

当＞0时，

解析

解析已在路上飞奔，马上就到！

知识点

弦切角与圆有关的比例线段绝对值不等式的解法不等式的证明

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷