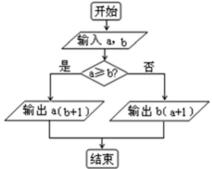
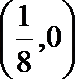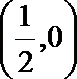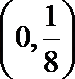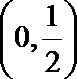- 真题试卷
- 模拟试卷
- 预测试卷
1.集合
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.抛物线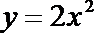
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.对于实数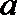

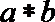
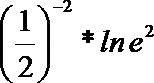
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.设

①若


③若



其中命题正确序号是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.以下茎叶图记录了甲、乙两组各6名学生在一次数学测试中的成绩(单位:分)。已知甲组数据的众数为124,乙组数据的平均数即为甲组数据的中位数,则

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 已知函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 线段








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.从6名教师中选5名开发A、B、C、D四门课程,要求每门课程有一名教师开发,每名教师只开发一门课程,且这6名中甲、乙两人不开发A课程,则不同的选择方案共有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.函数
①函数
②若


③函数
④

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 若直线




正确答案
- 4
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知函数


①任意实数
②存在实数
③该方程不可能只有1根;
④若该方程有四个根,则该四个根之和的范围是
其中正确的序号是
正确答案
①②④
解析
解析已在路上飞奔,马上就到!
知识点
12.小G和小M相约周末去欢乐谷游玩,他们约定周日早上8点至9点之间(假定他们在这一时间段内任一时刻等可能的到达)在欢乐谷正大门前集中前往,则他们中先到者等待的时间不超过15分钟的概率是
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 如图,在四边形






正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
14.若关于




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知等差数列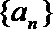

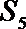
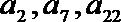
(Ⅰ)求数列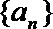
(Ⅱ)设数列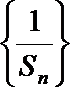
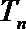
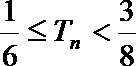
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,多面体





(Ⅰ)若点



(Ⅱ)求直线

(Ⅲ)在直线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 已知函数


(1)求
(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某单位从一所学校招收某类特殊人才.对
例如,表中运动协调能力良好且逻辑思维能力一般的学生有


(I) 求

(II)从参加测试的

(III)从参加测试的

生人数为


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,已知圆




(Ⅰ)求椭圆的方程;
(Ⅱ)若右焦点F在以线段CD为直径的圆E的外部,求m的取值范围。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(I)若函数

(Ⅱ)在(1)的条件下,若



(Ⅲ)设






正确答案
解析
解析已在路上飞奔,马上就到!