- 真题试卷
- 模拟试卷
- 预测试卷
3.左下图是某高三学生进入高三来的12次数学考试成绩的茎叶图,第1次到第12次的考试成绩依次记为:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知某几何体的三视图如图所示,则该几何体的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 设三位数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知正项等比数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知复数z满足

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.下列说法中,不正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 双曲线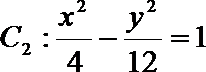
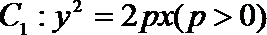
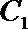
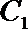
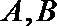
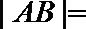
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知

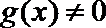
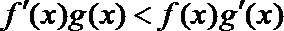
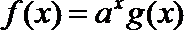
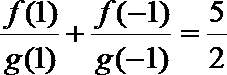
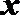

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知锐角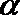
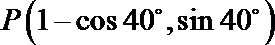

正确答案
70°
解析
解析已在路上飞奔,马上就到!
知识点
12.若

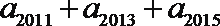
正确答案
122
解析
解析已在路上飞奔,马上就到!
知识点
13.若直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知正四面体

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数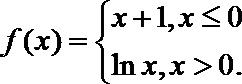
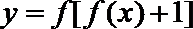
正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
16. 已知


(1)求
(2)若对


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 设数列






(1)求数列
(2)设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 随着人们对雾霾环境关注度的提高,绿色低碳出行越来越受到市民重视,为此成都市建立了公共自行车服务系统,市民凭本人二代身份证到公共自行车服务中心办理诚信借车卡借车,初次办卡时卡内预先赠送20分,当积分为0时,借车卡将自动锁定,限制借车,用户应持卡到公共自行车服务中心以1元购1个积分的形式再次激活该卡,为了鼓励市民租用公共自行车出行,同时督促市民尽快还车,方便更多的市民使用,公共自行车按每车每次的租用时间进行扣分收费,具体扣分标准如下:
①租用时间不超过1小时,免费;
②租用时间为1小时以上且不超过2小时,扣1分;
③租用时间为2小时以上且不超过3小时,扣2分;
④租用时间超过3小时,按每小时扣2 分收费(不足1小时的部分按1小时计算).
甲、乙两人独立出行,各租用公共自行车一次,两人租车时间都不会超过3小时,设甲、乙租用时间不超过一小时的概率分别是0.5和0.6;租用时间为1小时以上且不超过2小时的概率分别是0.4和0.2.
(1)求甲、乙两人所扣积分相同的概率;
(2)设甲、乙两人所扣积分之和为随机变量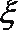
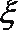
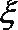
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图四棱锥













(1)求过点P,C,B,G四点的球的表面积;
(2)求直线

(3)在棱





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.椭圆






(1)若
(2)若椭圆的离心率满足


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(1)求实数
(2)求函数

(3)对于任意给定的正实数






正确答案
解析
解析已在路上飞奔,马上就到!