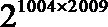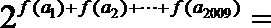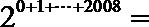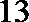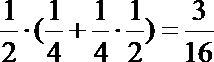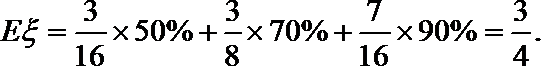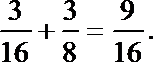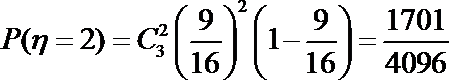- 真题试卷
- 模拟试卷
- 预测试卷
9.已知函数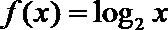
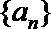


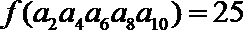
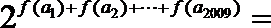
正确答案
解析
因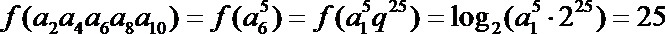
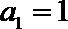
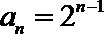
所以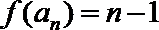
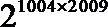
知识点
3.学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为



正确答案

解析



知识点
6.

正确答案

解析
首尾配对,如
故原式
知识点
8.某校选派









正确答案

解析
找出的学生是一男一女的概率为
知识点
10. 阅读下列材料:若两个正实数










正确答案
解析
构造函数





知识点
1.已知矩阵





正确答案
解析
由
知识点
2.函数



正确答案
解析
因




知识点
5.已知函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知







正确答案
解析

知识点
7.不等式


正确答案


解析
求函数


知识点
12.已知





正确答案
解析
令
由系数和


从而


易知
知识点
13. 已知以







正确答案
解析
由数形结合知,直线



知识点
14.定义函数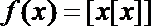
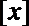
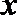
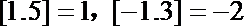
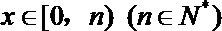
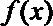
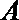
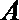
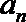
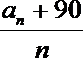
正确答案
解析
当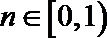
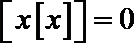
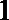
当
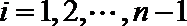
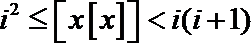

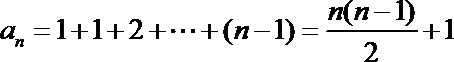
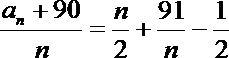
由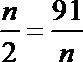
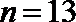
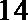
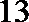
知识点
11. 已知抛物线










正确答案
解析
当直线

知识点
18.如图









正确答案
解析
当





知识点
15.“


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.若

正确答案
解析
令





知识点
17.对于数列






正确答案
解析
(A)的反例可以是:



(C)的反例可以是:


知识点
19.已知以角









(1)求角
(2)求
正确答案
(1)

且
由正弦定理
可得:

化简求得:

(2)



解析
解析已在路上飞奔,马上就到!
知识点
20.如图.一个小球从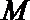
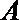
(1)求投入小球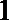
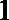
(2)已知获得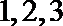
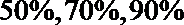
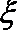
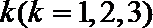
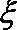
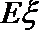
(3)若有
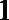
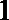
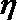
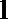
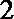
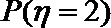
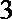
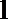
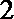
正确答案
(1)投入小球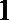
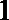
(2)由题意得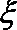
则
(3)由(2)可知,获得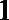
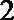
由题意得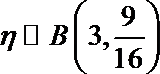
则
解析
解析已在路上飞奔,马上就到!
知识点
22.设数列





(1)求数列
(2)将数列











(3)设





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.如图,四棱锥






(1)求证:
(2)求

(3)求点

正确答案
∵

∴以


∵
∴ 
(1)∴

(2) ∵
设面
∴
∵

即

(3)∵
设面
设
∴点

解析
解析已在路上飞奔,马上就到!
知识点
23.已知抛物线


(1)求抛物线
(2)若过焦点




(3)求出一个数学问题的正确结论后,将其作为条件之一,提出与原来问题有关的新问题,我们把它称为原来问题的一个“逆向”问题。
例如,原来问题是“若正四棱锥底面边长为





现有正确命题:过点







试给出上述命题的“逆向”问题,并解答你所给出的“逆向”问题。
正确答案
(1)
(2)设

因为M、F、N共线,则有


所以

(3)“逆向问题”一:
①已知抛物线C:
过点F的直线交抛物线C于P、Q两点,
设点P关于x轴的对称点为R,
则直线RQ必过定点
证明:设过F的直线为y=k(x


则
由
得
所以



所以直线RQ必过焦点A。
②过点
③已知抛物线C:
“逆向问题”二:
已知椭圆C:

“逆向问题”三:
已知双曲线C:
解析
解析已在路上飞奔,马上就到!