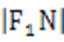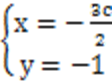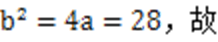- 真题试卷
- 模拟试卷
- 预测试卷
1.若复数z满足zi=1-i,则z等于()
正确答案
解析
∵
知识点
4.若


正确答案
解析
当








知识点
9.如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角












正确答案
解析
如图:过M作MD⊥OP于D,则 PM=




知识点
5.双曲线
正确答案
解析
双曲线


知识点
8.已知某运动员每次投篮命中的概率都为40%。现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器算出0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果。经随机模拟产生了20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为()
正确答案
解析
由随机数可估算出每次投篮命中的概率

知识点
2.等差数列



正确答案
解析
∵

知识点
3.函数
正确答案
解析
当


当


知识点
6.执行下图的程序框图,若输入的

正确答案
解析
输入








知识点
10.设函数



正确答案
解析
知识点
7.已知




正确答案
解析
设











知识点
11.(a+x)4的展开式中x3的系数等于8,则实数a=_________。
正确答案
2
解析
知识点
13.过抛物线


正确答案
2
解析
由题意可知过焦点的直线方程为


知识点
15.当x∈R,|x|<1时,有如下表达式:
1+x+x2+…+xn+…=
两边同时积分得:
从而得到如下等式:

请根据以上材料所蕴含的数学思想方法,计算:

正确答案
解析
由



知识点
12.若一个底面是正三角形的三棱柱的正视图如图所示,则其表面积等于()
正确答案
解析
由正视图知:三棱柱是以底面边长为2,高为1的正三棱柱,所以底面积为

知识点
14.如图,






正确答案
解析
由余弦定理

再由正弦定理


知识点
18.设


(1)记使得“

(2)设


正确答案
见解析。
解析
(1)由





(2)由于








所以

知识点
19.设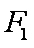
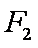
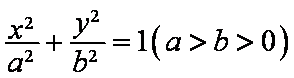
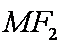
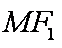
(1)若直线MN的斜率为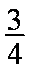
(2)若直线MN在y轴上的截距为2,且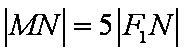
正确答案
见解析。
解析
(1)根据c=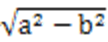

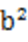
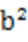
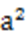
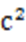
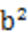



(2)由题意,原点O的
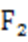
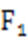
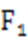

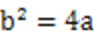
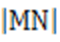
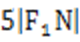
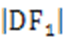
设N(x,y),由题意可知y<0,则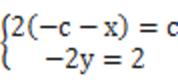
代入方程C,得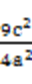

将①以及c=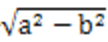
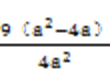

解得a=7,
a=7,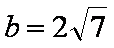
知识点
17.如图三棱柱


(1) 证明:
(2)若


正确答案
见解析。
解析
(1)连结










(2)因为

故OA⊥OB,从而OA,OB,
以O为坐标原点,OB的方向为x轴正方向,OB为单位长,建立如图所示空间直角坐标系O-






设


设

则


知识点
16.某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数。
(1)sin213°+cos217°-sin13°cos17°
(2)sin215°+cos215°-sin15°cos15°
(3)sin218°+cos212°-sin18°cos12°
(4)sin2(-18°)+cos248°- sin2(-18°)cos48°
(5)sin2(-25°)+cos255°- sin2(-25°)cos55°
(1) 试从上述五个式子中选择一个,求出这个常数
(2) 根据(1)的计算结果,将该同学的发现推广位三角恒等式,并证明你的结论.
正确答案
见解析。
解析
(1)选择(2)式计算如下:
(2)证明:
知识点
20.已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的周期为π,图象的一个对称中心为

(1)求函数f(x)与g(x)的解析式;
(2)是否存在x0∈
(3)求实数a与正整数n,使得F(x)=f(x)+ag(x)在(0,nπ)内恰有2 013个零点。
正确答案
见解析。
解析
(1)由函数f(x)=sin(ωx+φ)的周期为π,ω>0,得ω=
又曲线y=f(x)的一个对称中心为
故

将函数f(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)后可得y=cos x的图象,再将y=cos x的图象向右平移

(2)当x∈



所以sin x>cos 2x>sin xcos 2x.
问题转化为方程2cos 2x=sin x+sin xcos 2x在
设G(x)=sin x+sin xcos 2x-2cos 2x,x∈
则G′(x)=cos x+cos xcos 2x+2sin 2x(2-sin x)。
因为x∈

又

且函数G(x)的图象连续不断,故可知函数G(x)在
即存在唯一的x0∈
(3)依题意,F(x)=asin x+cos 2x,令F(x)=asin x+cos 2x=0.
当sin x=0,即x=kπ(k∈Z)时,cos 2x=1,从而x=kπ(k∈Z)不是方程F(x)=0的解,
所以方程F(x)=0等价于关于x的方程

令
则问题转化为研究直线y=a与曲线y=h(x),x∈(0,π)∪(π,2π)的交点情况。



当x变化时,h′(x),h(x)的变化情况如下表:
当x>0且x趋近于0时,h(x)趋向于-∞,
当x<π且x趋近于π时,h(x)趋向于-∞,
当x>π且x趋近于π时,h(x)趋向于+∞,
当x<2π且x趋近于2π时,h(x)趋向于+∞。
故当a>1时,直线y=a与曲线y=h(x)在(0,π)内无交点,在(π,2π)内有2个交点;
当a<-1时,直线y=a与曲线y=h(x)在(0,π)内有2个交点,在(π,2π)内无交点;
当-1<a<1时,直线y=a与曲线y=h(x)在(0,π)内有2个交点,在(π,2π)内有2个交点。
由函数h(x)的周期性,可知当a≠±1时,直线y=a与曲线y=h(x)在(0,nπ)内总有偶数个交点,从而不存在正整数n,使得直线y=a与曲线y=h(x)在(0,nπ)内恰有2 013个交点;
又当a=1或a=-1时,直线y=a与曲线y=h(x)在(0,π)∪(π,2π)内有3个交点,由周期性,2 013=3×671,所以依题意得n=671×2=1 342.
综上,当a=1,n=1 342或a=-1,n=1 342时,函数F(x)=f(x)+ag(x)在(0,nπ)内恰有2 013个零点。
知识点
21.本题设有(1)、(2)、(3)三个选考题,每题7分,请考生任选2题作答,满分14分。如果多做,则按所做的前两题计分。
(1)(本小题满分7分)选修4-2:矩阵与变换
设矩阵 


①若



②若曲线




(2)(本小题满分7分)选修4—4:坐标系与参数方程
在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,已知点A的极坐标为

①求a的值及直线l的直角坐标方程;
②圆C的参数方程为
(3)(本小题满分7分)选修4-5:不等式选讲:解不等式∣2x-1∣<∣x∣+1
正确答案
见解析。
解析
(1)
①设矩阵













②设曲线



则










(2)
①由点A


所以直线l的方程可化为ρcos θ+ρsin θ=2,从而直线l的直角坐标方程为x+y-2=0.
②由已知得圆C的直角坐标方程为(x-1)2+y2=1,所以圆C的圆心为(1,0),半径r=1,因为圆心C到直线l的距离d=

(3)当x<0时,原不等式可化为
又
当
又
当
综上,原不等式的解集为