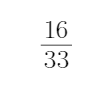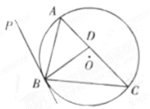- 真题试卷
- 模拟试卷
- 预测试卷
1. 设全集



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 设等比数列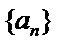
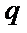
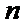
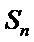
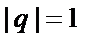
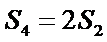
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 某地举行一次民歌大奖赛,六个省各有一对歌手参加决赛,现要选出4名优胜者,则选出的4名选手中恰有且只有两个人是同一省份的歌手的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 如图所示,正方体









①平面

②当且仅当x=
③四边形


④四棱锥

以上命题中假命题的序号为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 设a=20.3,b=0.32,c=log20.3,则a,b,c的大小关系是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
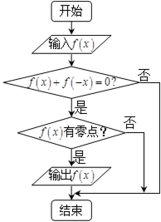
4.某流程图如图所示,现输入如下四个函数,则可以输出的函数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 一几何体的三视图如下:其体积为____________
正确答案
12(cm3)
解析
解析已在路上飞奔,马上就到!
知识点
9. 如图,在复平面内,复数




正确答案
二
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知直线




正确答案

解析
解析已在路上飞奔,马上就到!
知识点
13.已知双曲线C的中心在原点,焦点在坐标轴上,焦距为10,点P(2,1)在C的渐近线上,则C的方程为_________________________。
正确答案




解析
解析已在路上飞奔,马上就到!
知识点
14.已知A、B为函数






a


正确答案
d
解析
解析已在路上飞奔,马上就到!
知识点
10. 如图所示,直线PB与圆O相切于点B,D是弦AC上的点,∠PBA=∠DBA,若AD=m,AC=n,则AB=_________.
正确答案
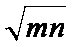
解析
解析已在路上飞奔,马上就到!
知识点
16.如图,PDCE为矩形,ABCD为梯形,平面
(Ⅰ)若M为PA中点,求证:AC//平面MDE;
(Ⅱ)求直线PE与平面PBC所成角的正弦值.
(Ⅲ)在PC上是否存在一点Q,使得平面QAD与平面PBC所成锐二面角的大小为
正确答案
(Ⅰ)连结



∵


∴
因为




(Ⅱ)∵

又



∴



以




设面

即:
得:
设


∴
(Ⅲ)设
设平面

即:
得:




所以,PC上存在点Q满足条件,Q与P重合,或
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数

(Ⅰ)已知函数


(Ⅱ)讨论函数
(Ⅲ)







正确答案
(Ⅰ)函数





因为函数

即



答案得
经检验:


(Ⅱ)




令



i、当2



所以






ii、当2







所以


iii、当0<2



所以






综上所述:
0<






















(Ⅲ)由题意,











由(Ⅱ)










所以

即
化简得


又



解析
解析已在路上飞奔,马上就到!
知识点
19.已知




(Ⅰ)求

(Ⅱ)若过








正确答案
(Ⅰ)依题意可知,








故



(Ⅱ)设



故
故
由

故
故
因为直线



当


当



解析
解析已在路上飞奔,马上就到!
知识点
15.已知



(Ⅰ)求角
(Ⅱ)求函数
正确答案
(I)由正弦定理,得:
即
故

所以
(II)

所以所求函数值域为
解析
解析已在路上飞奔,马上就到!
知识点
17.小型风力发电项目投资较少,开发前景广阔.受风力自然资源影响,项目投资存在一定风险.根据测算,IEC(国际电工委员会)风能风区的分类标准如下:
某公司计划用不超过100万元的资金投资于A、B两个小型风能发电项目.调研结果是:未来一年内,位于一类风区的A项目获利

b项目位于二类风区,获利35%的可能性为0.6,亏损10%的可能性是0.2,不赔不赚的可能性是0.2.
假设投资A项目的资金为



(Ⅰ)请根据公司投资限制条件,写出

(Ⅱ)记投资A,B项目的利润分别为





(Ⅲ)根据(Ⅰ)的条件和市场调研,试估计一年后两个项目的平均利润之和
正确答案
(I)
(Ⅱ)A项目投资利润
B项目投资利润
(Ⅲ)由(I)可知,当
解析
解析已在路上飞奔,马上就到!
知识点
20.正整数数列

(Ⅰ)写出数列
(Ⅱ)将数列




(Ⅲ)求最小的正整数

正确答案
(Ⅰ)




(Ⅱ)由(Ⅰ)可知


猜想使


对






归纳易得:

故当

因此
(Ⅲ)由(Ⅱ)可知,

则


由(*)式可知,当

因此,当

而当



进而考虑
由


故使得

解析
解析已在路上飞奔,马上就到!