- 真题试卷
- 模拟试卷
- 预测试卷
1. 复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知向量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 已知实数x,y满足
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知点P在曲线y=ex(e自然对数的底数)上,点Q在曲线y=lnx上,则丨PQ丨的最小值是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 下面四个条件中,使a>b成立的充要条件是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数f(x)=Asin(ωx+φ)(A,ω,φ)为常数,A>0,ω>0的部分图象如图所示,则f(0)的值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知等差数列{an}的前n项和为Sn,a4+a7+a10=9,S14﹣S3=77,则使Sn取得最小值时n的值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知A、B、C是球O的球面上三点,三棱锥O﹣ABC的高为2
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设F1,F2分别为双曲线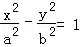
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.三棱锥的三组相对的棱(相对的棱是指三棱锥中成异面直线的一组棱)分别相等,且长各为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知f(x)=2sinx+x3+1,(x∈R),若f(a)=3,则f(﹣a)的值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知程序框图如图所示,当输入2与﹣2时,输出的值均为10,则输入1时输出的值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 设M,m分别是f(x)在区间[a,b]上的最大值和最小值,则m(b﹣a)≤

正确答案
[﹣16,0]
解析
解析已在路上飞奔,马上就到!
知识点
16.已知动圆的圆心C在抛物线x2=2py(p>0)上,该圆经过点A(0,p),且与x轴交于两点M、N,则sin∠MCN的最大值为___________.
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
13.各项均为正数的等比数列{an}的前n项和为Sn,a1=1,a2•a4=16则S4=_________
正确答案
15
解析
解析已在路上飞奔,马上就到!
知识点
14.天气预报说,在今后的三天中每一天下雨的概率均为40%,用随机模拟的方法进行试验,由1、2、3、4表示下雨,由5、6、7、8、9、0表示不下雨,利用计算器中的随机函数产生0〜9之间随机整数的20组如下:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
通过以上随机模拟的数据可知三天中恰有两天下雨的概率近似为_________
正确答案
0.25
解析
解析已在路上飞奔,马上就到!
知识点
19. 有一批货物需要用汽车从生产商所在城市甲运至销售商所在城市乙,已知从城市甲到城市乙只有两条公路,且通过这两条公路所用的时间互不影响.
据调查统计,通过这两条公路从城市甲到城市乙的200辆汽车所用时间的频数分布如下表:
假设汽车A只能在约定日期(某月某日)的前11天出发,汽车B只能在约定日期的前12天出发.
(I)为了尽最大可能在各自允许的时间内将货物运往城市乙,估计汽车A和汽车B应如何选择各自的路径;
(II)若通过公路1、公路2的“一次性费用”分别为3.2万元、1.6万元(其它费用忽略不计),此项费用由生产商承担.如果生产商恰能在约定日期当天将货物送到,则销售商一次性支付给生产商40万元,若在约定日期前送到,每提前一天销售商将多支付给生产商2万元;若在约定日期后送到,每迟到一天,销售商将少支付给生产商2万元.如果汽车A、B长期按(I)所选路径运输货物,试比较哪辆汽车为生产商获得的毛利润更大。
(注:毛利润=(销售商支付给生产商的费用)﹣(一次性费用))
正确答案
(I)频率分布表,如下:
设A1,A2分别表示汽车A在约定日期(某月某日)的前11天出发选择公路1,2将货物运往城市乙;B1,B2分别表示汽车B在约定日期(某月某日)的前12天出发选择公路1,2将货物运往城市乙.
∵P(A1)=0.2+0.4=0.6,P(A2)=0.1+0.4=0.5,∴汽车A选择公路1,
∵P(B1)=0.2+0.4+0.2=0.8,P(B2)=0.1+0.4+0.4=0.9,∴汽车A选择公路2;
(II)设X表示汽车A选择公路1,销售商支付给生产商的费用,则X=42,40,38,36
X的分布列如下:
∴E(X)=42×0.2+40×0.4+38×0.2+36×0.2=39.2
∴汽车A选择公路1时的毛利润为39.2﹣3.2=36.0(万元)
设Y为汽车B选择公路2时的毛利润,则Y=42.4,40.4,38.4,36.4
分布列如下
∴E(Y)=42.4×0.1+40.4×0.4+38.4×0.4+36.4×0.1=39.4
∵36.0<39.4
∴汽车B为生产商获得毛利润更大.
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数f(x)=alnx+

(I)求实数a的取值范围;
(II)若x1∈(0,


正确答案
(I)由f(x)=alnx+
得:
∵a≠0,令
∴g(0)=1>0.
令

则0<a<2.
(II)由(I)得:
设ax2﹣(2a+1)x+a=0(0<a<2)的两根为α,β,
则

当x∈(0,α)和(β,+∞)时,
函数f(x)单调递增;
当x∈

函数f(x)单调递减,
则f(x1)≤f(a),f(x2)≥f(β),
则f(x2)﹣f(x1)≥f(β)﹣f(α)=alnβ
=
=

令
则
则函数h(x)单调递增,
h(x)≥h(2)=2ln2+
∴
∵
则
∴f(x1)﹣f(x2)≥ln2+
解析
解析已在路上飞奔,马上就到!
知识点
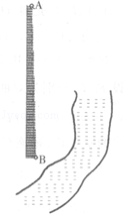
17.要测量河对岸的烟囱AB,而测量者又不能到达它的底部,现有测角仪和钢卷尺两种测量工具,请你设计一种测量方案.要求
(I)画出图形,指出要测量的数据(用字母表示并在图中标出);
(II)用文字和公式写出计算烟囱高AB的步骤(测角仪的高度忽略不计)
正确答案
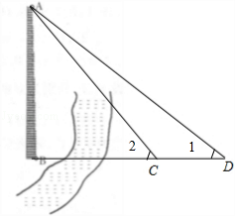
要测量河对岸的烟囱AB;如图:
(Ⅰ)在C出测得对烟囱AB的仰角∠2后退m米,在D处测得对烟囱AB的仰角∠1.
(Ⅱ)需要工具有测角仪与米尺.
在C出测得对烟囱AB的仰角∠2后退m米,在D处测得对烟囱AB的仰角∠1.
利用直角三角形列出关系式即可求出AB.

所以BC=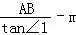

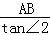
所以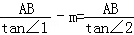
解得
AB=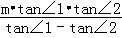
解析
解析已在路上飞奔,马上就到!
知识点
20.在平面直角坐标系xOy中,已知定点A(﹣2,0)、B(2,0),M是动点,且直线MA与直线MB的斜率之积为﹣
(I)求曲线C的方程;
(II )过定点T(﹣1,0)的动直线l与曲线C交于P,Q两点,是否存在定点S(s,0),使得
正确答案
(I)设M点坐标为(x,y)
∵定点A(﹣2,0)、B(2,0),直线MA与直线MB的斜率之积为﹣
∴
∴
∴曲线C的方程为
(II )当动直线l的斜率存在时,设动直线l的方程为y=k(x+1)(k≠0)
由
设P(x1,y1),Q(x2,y2),
∴
∵
∴
若存在定点S(s,0),使得

∴s=﹣
当动直线l的斜率不存在时,P(﹣1,



综上知,存在定点S(﹣

解析
解析已在路上飞奔,马上就到!
知识点
从22、23、24题中任选一题作答
22.选修4﹣1几何证明选讲
已知△ABC中AB=AC,D为△ABC外接圆劣弧,
(I)求证.∠CDF=∠EDF
(II)求证:AB•AC•DF=AD•FC•FB.
23.选修4﹣4坐标系与参数方程
在平面直角坐标系中,取原点为极点x轴正半轴为极轴建立极坐标系,已知曲线C1的极坐标方程为:ρ=2cosθ,直线C2的参数方程为:
(I )求曲线C1的直角坐标方程,曲线C2的普通方程.
(II)先将曲线C1上所有的点向左平移1个单位长度,再把图象上所有点的横坐标伸长到原来的
24.选修4﹣5不等式选讲
解不等式:
正确答案
22.证明:(I)∵A,B,C,D 四点共圆,∴∠ABC=∠CDF
又AB=AC∴∠ABC=∠ACB,
且∠ADB=∠ACB,∴∠ADB=∠CDF,7分
对顶角∠EDF=∠ADB,故∠EDF=∠CDF;
(II)由(I)得∠ADB=∠ABF
∵∠BAD=∠FAB
∴△BAD∽△FAB
∴
∴AB2=AD•AF
∵AB=AC
∴AB•AC=AD•AF
∴AB•AC•DF=AD•AF•DF
根据割线定理DF•AF=FC•FB
∴AB•AC•DF=AD•FC•FB
23.(I )C1的极坐标方程为:ρ=2cosθ,即:ρ2=2ρcosθ,
化为直角坐标方程为x2+y2=2x,即为(x﹣1)2+y2=1
直线C2的参数方程为:
消去t得普通方程为x﹣y+4=0
(II)曲线C3上的方程为
设点P(

由三角函数的性质知,
当


所以P点的坐标为(
24.①当x2﹣x<0时,即0<x<1时,不等式成立.
②当x2﹣x>0时,即 x>1 或 x<0时,不等式化为 x2﹣x≥|x|,故有﹣(x2﹣x)≤x≤x2﹣x,
解得 x≥2,或x≤0,
所以,x≥2或x<0.
故原不等式的解集为{x|x≥2或x<0或0<x<1}.
解析
解析已在路上飞奔,马上就到!
知识点
18.四棱锥的正视图和俯视图如图,其中俯视图是直角梯形.
(I )若正视图是等边三角形,F为AC的中点,当点M在棱AD上移动时,是否总有BF丄CM,请说明理由;
(II)若平面ABC与平面ADE所成的锐二面角为45°,求直线AD与平面ABE所成角的正弦值。
正确答案
(I)
若正视图是等边三角形,F为AC的中点,当点M在棱AD上移动时,总有BF丄CM.
取BC中点O,连接AO,
由俯视图可知,AO⊥面BCDE,
取DE中点H,连接OH,OH⊥BC
以OC、OH、OA分别为x,y,z轴,建立空间直角坐标系O﹣xyz,设A(0,0,
∴F(
设M(x,2x,
∴
∴
∴BF丄CM.
(II)D(1,2,0),设A(0,0,a)(a>0),
∴
设平面ADE的法向量为
∴
∴
∴可取
∵平面ABC的法向量为
∴
∵平面ABC与平面ADE所成的锐二面角为45°,
∴
设平面ABE的法向量为
∵
∴
∴
∴可取
∴
∴直线AD与平面ABE所成角的正弦值为
解析
解析已在路上飞奔,马上就到!