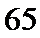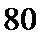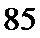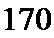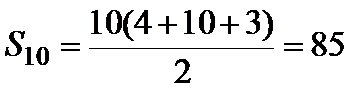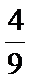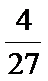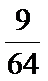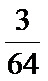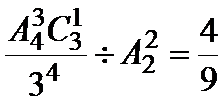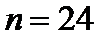- 真题试卷
- 模拟试卷
- 预测试卷
如图,在






17.求
18.求

正确答案
(1)
解析
在






考查方向
解题思路
在






易错点
余弦定理的边角关系对应错误导致计算出错
正确答案

解析
(2)由(1)得






考查方向
解题思路
在






易错点
诱导公式应用错误,导致
根据某水文观测点的历史统计数据,得到某河流水位

将河流水位在以上
19.求未来三年,至多有

20.该河流对沿河









正确答案
(1)
解析
在区间

考查方向
解题思路
【解题思路】先由频率分布直方图得到

易错点
题目看错,误认为只是求
正确答案
方案二较好
解析





考查方向
解题思路
损失由两部分构成:工程费用+超过的水位造成的影响
易错点
在计算损失的时候只考虑了河流对企业的影响,而忽略了工程费用
如图,在直角








28.证明:

29.若




正确答案
见解析
解析
如图,连接EF,BE,则因为AB是直径,
所以




而






所以




所以



考查方向
解题思路
证明四点共圆就是要证明四边形的对角互补,如图,证明

易错点
切割线定理记错,如
正确答案
解析
由切割线定理得
再在

再在

由切割线定理得
所以
考查方向
解题思路
证明四点共圆就是要证明四边形的对角互补,如图,证明

易错点
切割线定理记错,如
如图,四棱锥




21.求证:平面

22.若

正确答案
(1)证明略
解析
如图,取AB中点O,连接CO,PO,BC=AB=2,
所以

在
所以
所以满足
所以

所以
又因为
所以平面

考查方向
解题思路
取AB中点O,连接CO,PO,求得CO=




第二问,以O点为坐标原点建立空间直角坐标系,分别写出点的坐标,然后求出两个面的法向量,用向量法可求。
易错点
在第一问做图的时候不是取得AB中点,而是做了AB垂线,导致PO长度不可求,以致于最后少一组垂直,无法证明;
正确答案
解析
如图,以O点为坐标原点,建立空间直角坐标系,
设平面APC的法向量为
得到
设平面DPC的法向量为
得到
由图可知,这两个面所成的二面角为锐二面角,所以所求的余弦值为
考查方向
解题思路
以O点为坐标原点建立空间直角坐标系,分别写出点的坐标,然后求出两个面的法向量,用向量法可求。
易错点
想尝试综合法(几何法)解决,结果无法做出二面角的平面角.
只有当两个面中有一个是平行或垂直于底面的时候,我们才适合用综合法(几何法)做,其它都用空间向量解决.
已知椭圆



23.求

24.直线





正确答案
(1)
解析
(1)








考查方向
解题思路
第一问根据离心率得到
易错点
在最后计算求最值得时候没有进行合理的换元,导致无法求出最值
正确答案
解析
为避免讨论直线斜率不存在的情况,直接设直线



即
得到
由判别式大于0可以得到
设直线



则
由根与系数的关系得到
所以
令

所以,当且仅当
考查方向
解题思路
【解题思路】第一问根据离心率得到
易错点
第二问在设方程的时候设为
已知函数


25.求函数
26.判断函数
27.若函数


正确答案
(1)增区间
解析






考查方向
解题思路
第一问直接求导,解不等式即得。
易错点
在分类的时候没有找准分类的标准,而导致后面逻辑混乱
正确答案
见解析
解析
当


















当

当










当













考查方向
解题思路
当
当


且
所以


当
当
当





当

当

当


所以存在唯一














综上,当



易错点
第二问误解题目意思,试图求出零点
正确答案
见解析
解析
由(2)知,当




















考查方向
解题思路
由(2)知,当




















易错点
在分类的时候没有找准分类的标准,而导致后面逻辑混乱
8.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,
则在该几何体中,最长的棱的长度是( )
正确答案
解析
底面为直角梯形,上底,下底和高分别为2,4,4,四棱锥的高为4,则最长棱为俯视图中的梯形中的对角线,长度为
考查方向
解题思路
根据三视图画出直观图,可以看出该几何体为一个四棱锥,然后根据各边长判断出最长棱,并求长度
易错点
1、不能根据三视图画出直观图2、最长棱判断错误
1.已知集合


正确答案
解析
由集合A得




考查方向
解题思路
集合A要求根号里面的式子大于或等于0,集合B需要真数大于0且小于等于2,然后取交集即可
易错点
忽略对数函数的真数应该大于0
知识点
2.设




正确答案
解析
两边同除以


考查方向
解题思路
两边同除以虚数单位


易错点
复数的除法运算是要分子分母同乘以共轭复数
知识点
3.已知平面向量








正确答案
解析




考查方向
解题思路
先计算


易错点
忽略了

知识点
5.公差为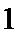
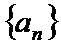
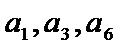
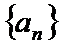
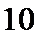
正确答案
解析
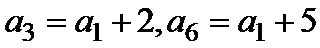
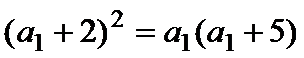
解得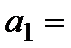
所以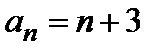
考查方向
解题思路
根据等差数列的定义,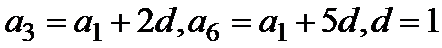
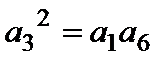

易错点
不知道等比中项的性质,或把等比中项与等差中项混淆
知识点
7. 
正确答案
解析

所以常数项为
考查方向
解题思路
第一步,求第二个式子展开式中
易错点
1、常数项的来源有两种,一种是前面因式中的

知识点
10.点










正确答案
解析




考查方向
解题思路
如图,M为



易错点
1、
知识点
12.函数

正确答案
解析
首先构造两个函数


(1)当

(2)当

(3)当



考查方向
解题思路
首先构造两个函数


易错点
1、忽略对数函数的定义域导致结果出错
2、没有注意到后面的二次函数过原点,而增加不必要的讨论和计算
知识点
4.若


正确答案
解析
如右图,不等式组表示的可行区域为


考查方向
解题思路
先画出不等式表示的可行区域,然后将目标函数变形成

易错点
1、对不等式表示的是直线的哪边部分认识不清
2、对目标函数的几何意义不了解
知识点
6.若函数

正确答案
解析
将

得到
得到
又因为
所以
求对称轴,
解得
考查方向
解题思路
将


易错点
1、正弦值为

2、忽略题中给出的、忽略题中给出的
知识点
9.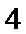
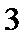

正确答案
解析
首先计算总数,4个人,每个人都可以在3项不同的活动中任选一项,也就是每个人都有3中选择,所以总数是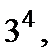
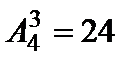
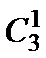
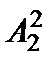
考查方向
解题思路
首先根据邮筒原理,算出总数,然后来计算每一项至少有一人参加共有多少种,最后计算概率
易错点
1、总数是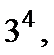
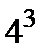
2、不会计算每项至少有一人参加的数量
知识点
11.过点






正确答案
解析
过点


解得
考查方向
解题思路
因为双曲线是无限接近于它的渐近线的,所以双曲线到直线的距离恒大于
易错点
不能将曲线到直线的距离转化成直线到直线的距离,导致计算繁琐甚至出错
知识点
15.过抛物线


交于



正确答案
解析
根据题意可以知道直线AB的斜率








考查方向
解题思路
根据题意可以知道直线AB的斜率为1,过点
易错点
垂直平分,只注意到了垂直而忽略了中点问题,导致无法计算
13.已知




正确答案
解析
把






考查方向
解题思路
把



易错点
忘记函数奇偶性的定义,导致无法进行变形计算
知识点
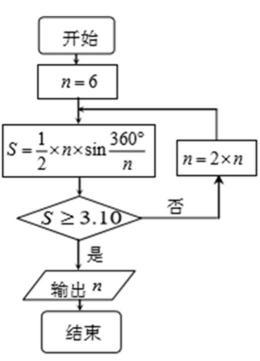
14.公元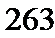
限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”,利
用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值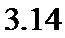
就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程
序框图,则输出的值为_______
(参考数据: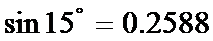
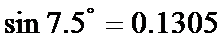
正确答案
24
解析
第一步: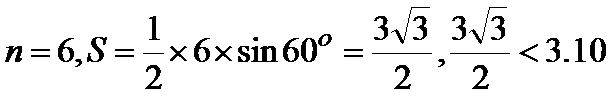
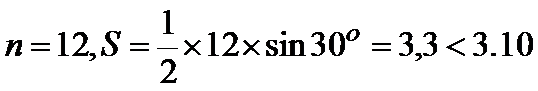
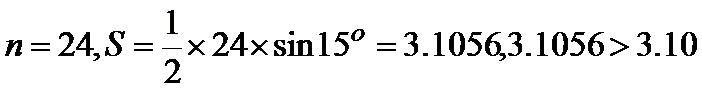
考查方向
解题思路
根据程序框图的计算顺序一步一步计算,逐步得到结果
易错点
程序框图理解错误,填写了S的输出值
知识点
16.数列



正确答案
解析
第一种情况:当

第二种情况:当











考查方向
解题思路
由分段函数可知,若数列为等比数列,则它的公比为2,要使得数列是公比为2的等比数列,则从数列的第二项开始,都应该满足分段函数的2式,也就是
易错点
不能理解分段函数的意思