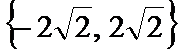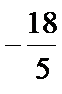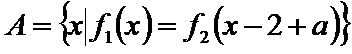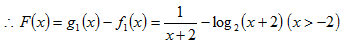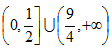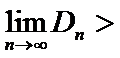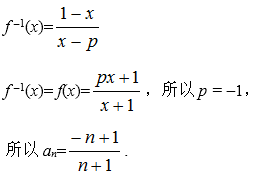- 真题试卷
- 模拟试卷
- 预测试卷
3.设等差数列




正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
9.已知圆锥的底面半径


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若行列式

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.集合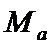
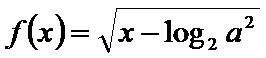
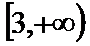

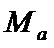
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若经过点P(-1,0)的直线与圆
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.含有三个实数的集合可表示为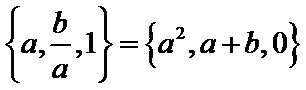

正确答案
-1
解析
解析已在路上飞奔,马上就到!
知识点
7.设函数








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知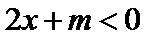
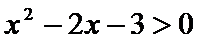

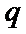
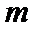
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知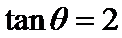

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.在平面直角坐标系中,x轴正半轴上有5个点, y轴正半轴有3个点,将x轴上这5个点和y轴上这3个点连成15条线段,这15条线段在第一象限内的交点最多有( ) 个
正确答案
30
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数






正确答案

解析
解析已在路上飞奔,马上就到!
知识点
13.已知









正确答案
18
解析
解析已在路上飞奔,马上就到!
知识点
15.如下图所示的程序框图的输出结果是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.四棱柱成为平行六面体的充分不必要条件是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.点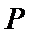
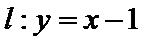
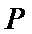


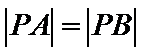
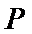
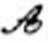
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
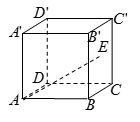
20.如图所示,已知单位正方体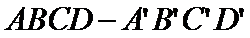
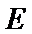
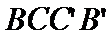
(1)求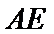
(2)求异面直线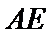
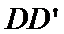
(3)求二面角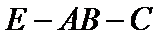
正确答案
(1)过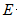
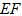
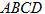

∴ 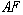
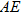
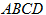
∴∠ 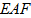
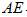
∴在 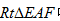
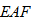

因此,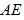
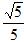
(2)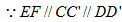
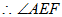
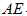
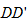
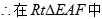
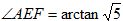
因此,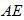
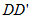
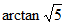
(3)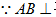
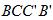
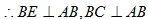
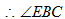
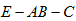
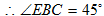
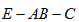
解析
解析已在路上飞奔,马上就到!
知识点
19.在


(1)求
(2)若


正确答案
(1)由
得
即



∴

(2)


解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数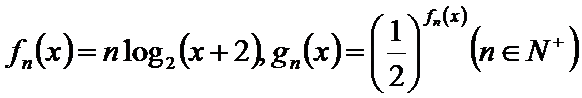
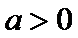
(1)确定实数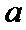
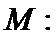
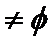
(2)确定实数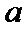
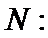
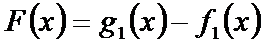
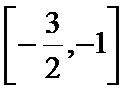
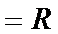
(3)如果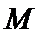
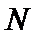

正确答案
(1)方程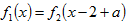
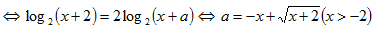
令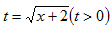
则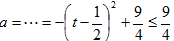
故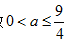
(2)又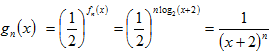
由于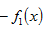
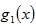
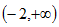
故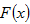
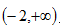
而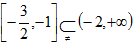
故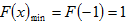
依题意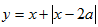
而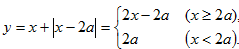
则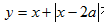
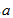
因此,若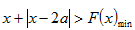
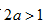
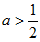
(3)如果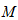
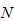
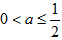
如果


故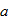
解析
解析已在路上飞奔,马上就到!
知识点
23.由函数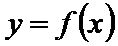
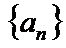
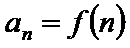
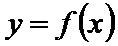
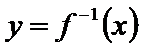
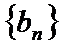
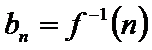
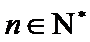
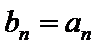
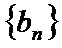
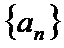
(1)若函数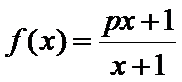
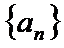
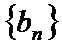

(2)已知正数数列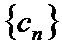
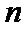
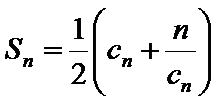

(3)在(1)和(2)的条件下,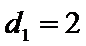
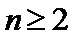
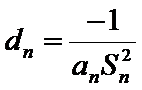
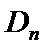

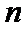
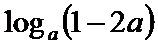
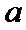
正确答案
(1)由题意得:
(2)因为正数数列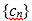
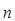

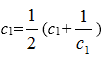
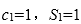
当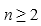
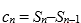
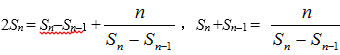
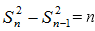
所以,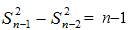
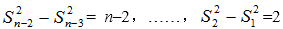
累加得:
(3)在(1)和(2)的条件下,
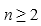
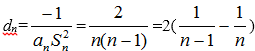
由


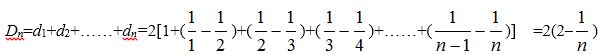
因为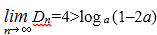
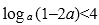
1–2a>0,所以0<a<0.475
解析
解析已在路上飞奔,马上就到!
知识点
22.已知二次曲线Ck的方程:
(1)分别求出方程表示椭圆和双曲线的条件;
(2)若双曲线Ck与直线
(3)设









正确答案
(1)当且仅当
即
当且仅当
即
(2)解法一:
∵双曲线实轴最长,∴

此时双曲线方程为
解法二:若

不妨设双曲线方程为
联立
得
∴实轴最长的方程为
解法三:不妨先求得


设直线与双曲线左支交点为
∴实轴最长的方程为
解法四:设双曲线与直线公共点为
则
即

∴实轴最长的方程为
(3)由(1)知

结合图像的几何间无公共点,任意两双曲线之间也无公共点,
设
则根据椭圆、双曲线定义及


所以
所以这样的
且
解析
解析已在路上飞奔,马上就到!